非对称加密
-
RSA 加密算法,一种非对称加密算法,在各种场景与环境下都有它的身影,那么它和其它加密算法又有什么不同呢,以及什么是非对称加密算法?
-
非对称加密:传统的加密算法基于同一密钥进行加密和解密,此时我们会发现我们攻击的重点将落在通信双方的密钥到底是什么,因为即使你的加密算法天衣无缝,但是你的密钥泄露了,我便可以直接通过解密算法得到密钥。
在一个不安全的通信环境中,你的信息需要经过很多节点(中间人)才能传输至目标,此时我们考虑两个问题:- 如何保证发送的信息没有被窃取?
- 如何保证是可信的发送人(即别人不能伪造你的身份发送信息)?
其实这便是信息安全等级保护中的CIA三要素的机密性(Confidentiality)和完整性(Integrity)要求。
显然,依靠传统的对称密码我们没办法做到这两点,因为传统对称密码需要事先约定使用某个特定的密码进行通信。此时我们考虑这样一个加密算法,它拥有两组密钥
公开密钥Pk(Public key):又称公钥,可以公开给所有人进行存储。
私有密钥Sk(Secret key):又称私钥,只能是发送者自己保存。 -
如果我们规定加密时使用公钥,解密时使用私钥,那么似乎我们的第一个问题中的放窃取便有了解决方案
我Xenny要给Soar发送信息,此时我只需要获取Soar的公开密钥(因为这会公开给所有人),然后用这个公钥将我们的信息进行加密,再发送给Soar即可,Soar收到信息后只需要用自己的私钥解密即可。
为什么?
考虑此时有一个中间节点获取了我们的信息,但是他只能得到加密的信息,而解密则需要私钥,故他没有窃取我们的消息。 -
那么如何保证可信呢,这里其实属于数字签名的内容,在后续的课程中我们会详细介绍各类签名、认证算法,那么在这里我们可以稍作提及,其实我们只需要使用私钥对数据进行签名,用公钥进行验签即可。
此处若不能理解如何操作,可以暂时不用深究。
RSA
- 在刚才的内容中,我们提到了非常多的新名词
公钥、私钥、非对称、签名等等…
但我们如何实现这种算法呢,让我们回到本节内容的重点——RSA算法上,RSA 是 1977 年由罗纳德 · 李维斯特(Ron Rivest)、阿迪 · 萨莫尔(Adi Shamir)和伦纳德 · 阿德曼(Leonard Adleman)一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
整个密码学的基石都是基于一些数学难题,以RSA算法为例,其基于大整数分解难题(IFP),目前来说我们并没有什么有效的办法对一个极大整数做因式分解,再多的优化在极大整数面前都与爆破无异,这保障了RSA的安全性。
接下来我们将学习RSA是如何工作的
生成公私钥

可能此时你便已经开始看不懂了,没关系,让我们一一拆分解释,值得注意的是,你会发现不同的资料上的表述可能都不太一样,例如“素”和“质”的区分,实际上,这些内容因为在目前我们无须深究,所以只需要了解其含义即可,再之后的教程中我们会学习各类算法在不同环、域上的扩展,此时我们再来深究其数学意义。

加密
- RSA算法本质上都是基于数学运算,在加密时我们需要先将消息转化为一个数字 m(例如消息ASCII码的二进制排列转为数字),然后有
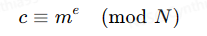
- 此时得到的 c 便是我们的密文。
解密
- 加密时我们只用到了公钥 (N,e),同理解密时我们也只需用到私钥 (N,d)。有
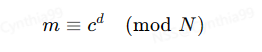
此时得到的 m 便是我们的明文消息。
正确性证明
- 也许此时你不明白为什么 m 能经过不同的两次幂运算后会得到原始值,这其实就是为什么RSA中要用到欧拉函数,如果你还不能够理解上面的一切,下面的正确性证明可以先略过,不要给自己徒增压力
转换为证明

算法实现
- 再上一节中我们学习了RSA的数学原理基础,本节课我们将了解如何具体实现RSA算法。
注意,在大部分资料中,其他作者更喜欢使用举一些特定的数字带入运算,从而让读者明白整个流程或从数字上直观的得到不同算式之间的联系。但我不会在这里不会使用此方式来阐述RSA的算法流程,带入具体数值进行计算观察关系的方式在解题时非常有效,但更多的我希望各位能够理解一种抽象的思维,这对我们后续的学习非常有帮助,当然各位同学在学习过程中可以自行选择自己喜欢的方式进行操作。
我们使用Python语言来实现一个RSA算法,首先你需要确保你已经安装好了Python执行环境以及编辑环境。(这一步如果有问题请自行搜索解决)
我使用的环境为Python 3.9.12+VSCode,你并不需要和我的环境保持一致,你可以选择自己熟悉或喜爱的环境进行操作,不过Python请使用3.8及以上版本,不然某些操作可能会得到不一样的结果。环境除了这二者之外还包括操作操作系统,我在平时工作中会使用很多不同的操作系统进行工作,对于CTF中密码学而言,这没那么重要,同时我也会尽量保持使用跨平台的代码。在特殊时候会进行进一步说明。
因为课程设置关系,在后续的内容中,我默认你已经基本掌握了Python语法,我将只会解释代码中新出现的库、函数、类的用法和说明。
Python实现RSA
- 上一节我们发现RSA无外乎就是那几个参数之间的运算,而我们要做的便是使用Python实现这些算式,首先我们要做的第一步是
-
生成两个大素数P,Q。
这是一个很模糊的概念,我希望各位在学习中能够做到尽量严谨,很显然,这里定义的大素数到底多大才是大呢?
10算大吗?100算吗?10000算吗?葛立恒数算吗?
我们需要一个更加精确的说法,我们生成两个512位的素数(这里包括之后的内容中涉及到的位都是指二进制位而不是十进制),那么如何使用Python产生一个素数呢,如果不借助任何外力的情况,我们可以从1开始选择,2,3,4…直到某个数满足512位且为素数为止,但是既然我们都使用Python了,为何还要这样做呢?
让我们来使用Python强大的开源库pycryptodome,一般来说你只需要使用pip3 install pycryptodome # 或 python3 -m pip install pycryptodome便可以成功安装,然后在Python环境中执行以下代码
import Crypto如果没有显示
ModuleNotFoundError:等诸如此类的错误话,那么恭喜你成功的安装了本库。这里你可能会奇怪为什么安装使用pycryptodome,而引入时使用Crypto,这涉及到这的库和其他库的一些联系,有兴趣的可以自行去查找。
然后我们就可以生成素数了,我们引入库中的子包Crypto.Util.number,这个子包中包含了大量的数学工具,之后我们会经常用到这个子包。from Crypto.Util.number import * p = getPrime(512) q = getPrime(512) print(p) print(q)执行上面的代码,你便可以得到两个512位的素数,这依赖于我们调用了包中的
getPrime函数,它能够返回一个n位的素数,其中n是我们的传入参数。至此我们便完成了RSA的第一步。
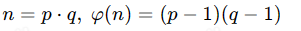
后续的过程便简单了很多,我们只需要在之前的基础上完成运算即可,添加下列代码并执行
n = p*q
phi = (p-1)*(q-1)- 选取与φ(n)互素的e,计算满足ed ≡ 1(mod φ(n))
这里我们要完成两个数学操作,一个是互素的判断,一个是求解e的乘法逆元。
e = 65537
assert GCD(e, phi) == 1, "该e不满足互素条件"
d = inverse(e, phi)这里GCD函数能够求解最大公因数(Greatest Common Divisor),之前我们学习了互素的概念就是两个数的最大公因数为1,所以这里我们用断言表达式认定e一定是和phi互素的。为什么我们要选择65537作为e呢,实际上这并不是硬性规定,一些标准提供了一些e的参考值,65537在各类实现与标准中被广泛使用,但是这并不影响你可以将值改变为其他值进行后续的操作。
求d的过程中,我们使用了inverse函数,该函数有两个参数(a,p),作用便是求解a在模p意义下的乘法逆元,那么这里我们便是求解e在模phi下面的乘法逆元,结果为d。之前我们提到了逆元是互为逆元,所以你可以尝试下面的代码
print(inverse(d, phi) == e)
打印的结果将为True,从这里我们也可以看出在RSA中的关键点便是获取这个phi的值,因为得到的phi我们便可以求e或d的值,而这正是我们加解密的密钥参数。
4.(n,e)即为公钥,(n,d)即为私钥,此时我们便得到了一组RSA的公私钥,随后我们便可以开始用这组密钥来进行加解密操作。
加密:
假设我们要加密的消息为Hello,我们定义一个字符串进行存储
message = b'hello'注意这里我们定义的是一个bytes类型字符串,它将每个字符用8位二进制进行存储,是字符串最原生的存储形式。你也可以直接定义'hello',但在Python3中它是一个Unicode的字符串,需要进行编码操作才能转换为bytes类型进行后续的运算。
但我们在RSA中是数与数的运算,该如何将字符串参与操作呢?
我们使用包中的bytes_to_long函数,从函数名也可以猜出来,这个函数是将字符串转换为数字,运行下列代码
m = bytes_to_long(message)
print(m)此时,我们的消息已经被转换为一个字符串了。随后我们便可以对消息进行RSA加密
c = pow(m, e, n)
print(c)我们使用Python自带的pow函数进行幂运算,注意不要写成m**e % n,二者代表的意义相同,但是pow函数内置快速幂,可以快速得出结果,而m**e % n会将me的结果先计算出来再取模,m的e次方是一个非常大的数,这会消耗你计算机大量的运算和存储资源。
至此,我们便完成了加密过程,得到了RSA的密文C。
解密:
我们执行
msg = pow(c, d, n)
print(msg)此时我们便完成了RSA的解密操作,随后你可以比较一下msg和m的值,他们会是一样的。
-
完整代码:
from Crypto.Util.number import * p = getPrime(512) q = getPrime(512) n = p*q phi = (p-1)*(q-1) e = 65537 assert GCD(e, phi) == 1, "该e不满足互素条件" d = inverse(e, phi) print(f'公钥:({e}, {n})') print(f'私钥:({d}, {n})') message = b'hello' m = bytes_to_long(message) print('消息:', m) c = pow(m, e, n) print('密文:', c) msg = pow(c, d, n) print('明文:', msg) assert msg == m, "解密失败"
帮助网站:n反查pq: http://factordb.com/

此处评论已关闭