DSA算法介绍
-
DSA全称为Digital Signature Algorithm(电子签名算法),被美国NIST选为DSS即Digital Signature Standard(电子签名标准)算法。
-
课程Crypto入门——RSA(一)的两个问题
- 如何保证发送的信息没有被窃取?
- 如何保证是可信的发送人(即别人不能伪造你的身份发送信息)?
-
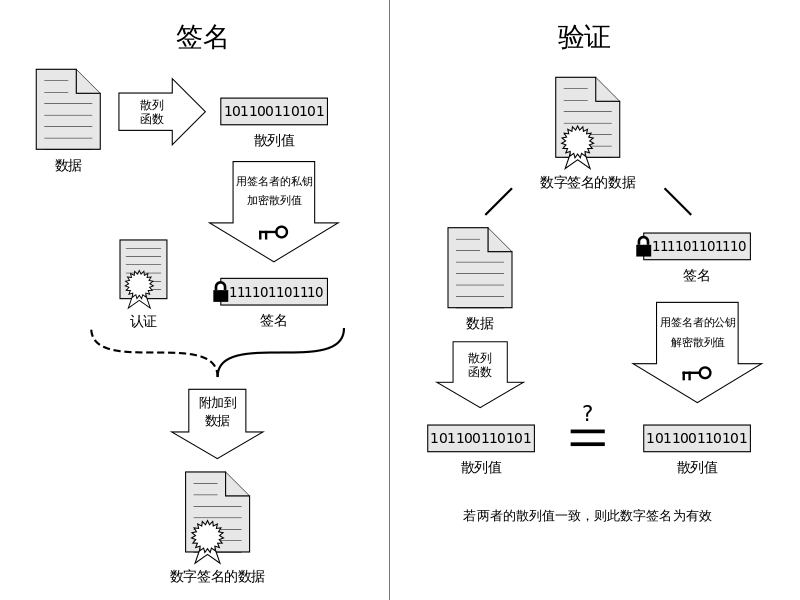
好的签名应该满足:
- 可鉴权
- 不可伪造
- 不可复制
- 不可篡改
- 不可抵赖
密钥生成

签名

验签

正确性证明
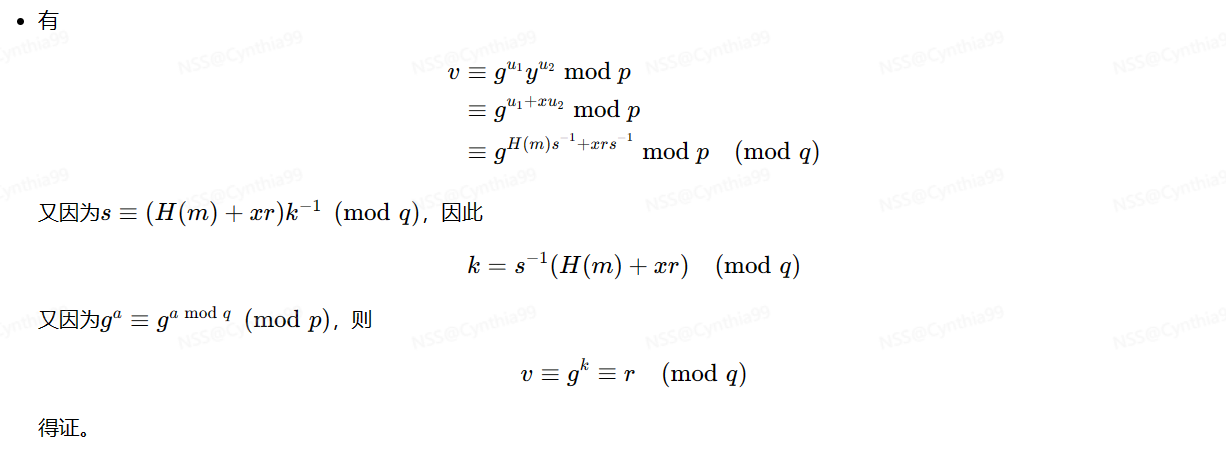
离散对数问题

暴力破解
- 枚举x得到正确的值。

def bsgs(g, y, p):
m = isqrt(p)+1
S = {powmod(g, j, p): j for j in range(m)}
gs = powmod(g, p - 1 - m, p)
for i in range(m):
if y in S:
return i * m + S[y]
y = y * gs % p
K相关攻击
已知K攻击

from Crypto.Util.number import *
k = 516081660287290857303106041337362876434325919397
p, q, g, y, h, r, s = ...
x = (s*k - h) * inverse(r, q) % q
print(long_to_bytes(x))K爆破攻击
- 如果题目中的k选择范围很小或是有迹可循,则可以考虑枚举每一个K的取值可能。转换为已知K攻击求解X。
from Crypto.Util.number import *
p, q, g, y, h, r, s = ...
for k in range(999900, 2**20): # 999957
x = (s*k - h) * inverse(r, q) % q
if long_to_bytes(x).count(b'-') == 2:
print(long_to_bytes(x))K共享攻击
- 如果在题目中包含多组签名且至少有两组签名使用了相同的临时密钥k,则我们依然可以从中计算得到x。
考虑约束

from Crypto.Util.number import *
p, q, g, y = ...
(h1, r1, s1) = ...
(h2, r2, s2) = ...
k = (h1 - h2) * inverse(s1 - s2, q) % q
x = (s1*k - h1) * inverse(r1, q) % q
print(long_to_bytes(x))K相关攻击进阶
线性K攻击

from Crypto.Util.number import *
from sympy.ntheory import *
p, q, g, y = ...
(h1, r1, s1) = ...
(h2, r2, s2) = ...
a = 123123
b = 213123
k = (h1*r2 - h2*r1 + b*s2*r1) * inverse(s1*r2 - a*s2*r1, q) % q
x = (k*s1 - h1) * inverse(r1, q) %q
print(long_to_bytes(x))关系K攻击

from Crypto.Util.number import *
p, q, g, y = ...
(h1, r1, s1) = ...
(h2, r2, s2) = ...
PR.<x> = PolynomialRing(GF(q))
f = s2*x^2*r1 - s1*x*r2 - h2*r1 + h1*r2
print(f.roots())
k = int(f.roots()[1][0])
x = (s1*k - h1) * inverse(r1, q) % q
print(long_to_bytes(x))
1 条评论
11111111