流密码LCG（线性同余生成器）

流密码

• 在密码学中，流密码是一种基于流加密算法的密码系统。与块密码不同，流密码将数据作为连续的比特流进行加密处理，以产生加密的比特流输出。流密码以其高速性和实时性能而在许多应用中得到广泛应用，例如通信系统、无线通信和网络安全等领域。
  流密码使用密钥和伪随机数发生器（PRNG）生成一个比特流序列，称为密钥流（key stream）。密钥流与明文比特流进行逐比特异或运算，从而实现加密或解密操作。密钥流的生成需要一个初始密钥作为输入，并通过PRNG生成器产生伪随机数序列。这种结合密钥流和异或运算的方式使得流密码具有高效且可逆的特性。

LCG

• 在之前的内容中，我们介绍了同余的概念，取模运算在密码学中经常被使用。本篇将向大家介绍另一个常见的密码学算法——线性同余生成器（Linear Congruential Generator，简称LCG）。
  线性同余生成器是一种伪随机数生成算法，可以生成一个看似随机的序列。其基本原理可以用下面的公式表示：
  
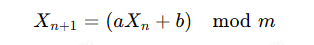
• 其中，Xn​表示第n个生成的随机数，a、b和m是事先选定的常数。初始值0X0​被称为种子值。

参数选择

LCG的性质与参数的选择密切相关，不同的参数可能导致不同的随机序列。一般按照如下要求选择对应的参数：

1. m是生成序列的模数，必须是一个大于0的正整数。常见的选择是使用一个较大的素数或2的幂，以提供较长的周期长度。
2. a是乘法因子，必须是一个与m互素的正整数。
3. b是增加常数，也必须是一个与m互素的正整数。

应用与安全性

• LCG算法在密码学中有广泛的应用，例如生成随机密钥、伪随机序列等。然而，需要注意的是，由于LCG算法的确定性特性，当参数选择不当时，可能导致序列出现可预测性，从而降低安全性。
  为了提高安全性，通常需要选择合适的参数，并使用其他的技术和算法来增加随机性。现代密码学中更倾向于使用更安全的随机数生成算法，如密码学安全伪随机数生成器（CSPRNG）。
  LCG的原理非常简单，我们也很容易写出它的Python代码实现

class LCG:
    def __init__(self, seed, a, b, m):
        self.seed = seed  # 初始种子
        self.a = a  # 乘数
        self.b = b  # 增量
        self.m = m  # 模数

    def generate(self):
        self.seed = (self.a * self.seed + self.b) % self.m
        return self.seed