• 最长公共子序列（LCS）的特征：
1、序列可连续，可不连续。
2、序列讲究顺序
3、答案不一定是唯一一个（有可能多个）
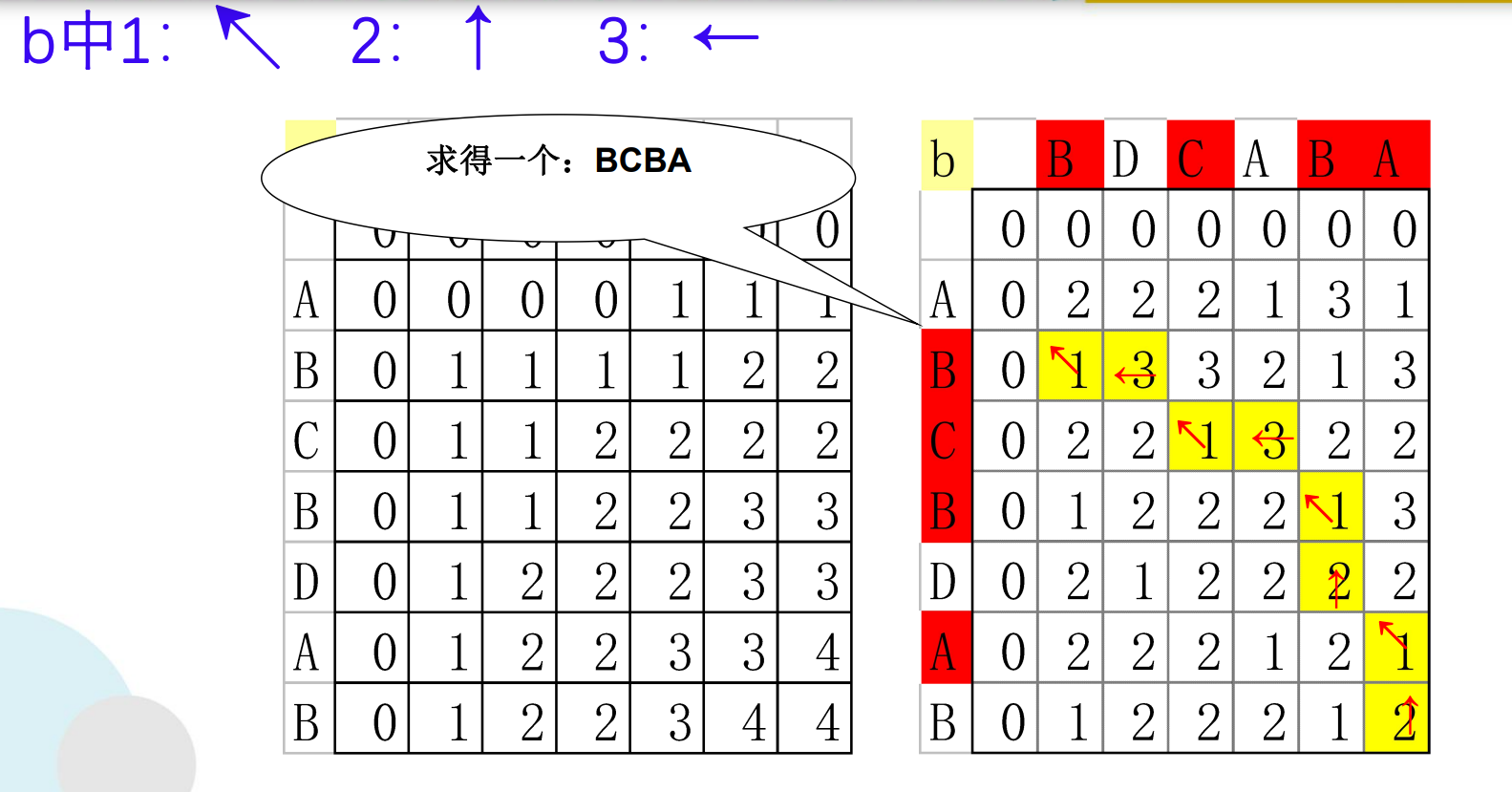
例如: X={ABCBDAB} ，Y={ BDCABA } 最长公共子序列有{BCBA}，{BDAB}，{BCAB}

穷举法：求LCS

• 若要求两个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列，先
取得X，Y的所有子序列，并进行一一比较，共有如下不同的组合：

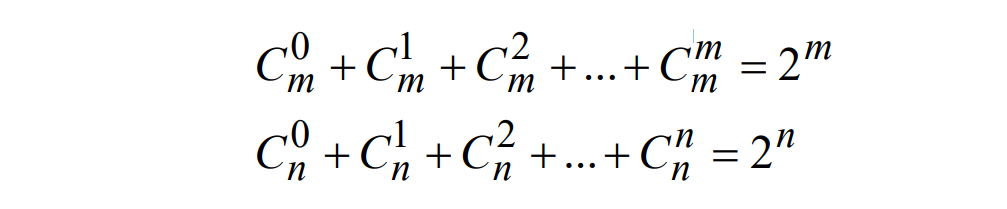
• X共有 个不同子序列， Y共有 个不同子序列，
• 共要进行不同的比较：2m+n 次
• 可见穷举法产生指数级的时间复杂度为O(2m+n )，因此，对于长序列，这种方法不可行。

最长公共子序列的结构

设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ，则
(1)若xm=yn，则zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列。
(2)若xm≠yn且zk≠xm，则Z是xm-1和Y的最长公共子序列。
(3)若xm≠yn且zk≠yn，则Z是X和yn-1的最长公共子序列。

由此可见，2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此，最长公共子序列问题具有最优子结构性质

子问题的递归结构

由最长公共子序列问题的最优子结构性质建立子问题最优值
的递归关系。用c[i][j]记录序列和的最长公共子序列的长度。
其中， Xi={x1,x2,…,xi}；Yj={y1,y2,…,yj}。当i=0或j=0时，空序列是Xi和Yj的最长公共子序列。
故此时C[i][j]=0。由最优子结构性质可建立递归关系如下

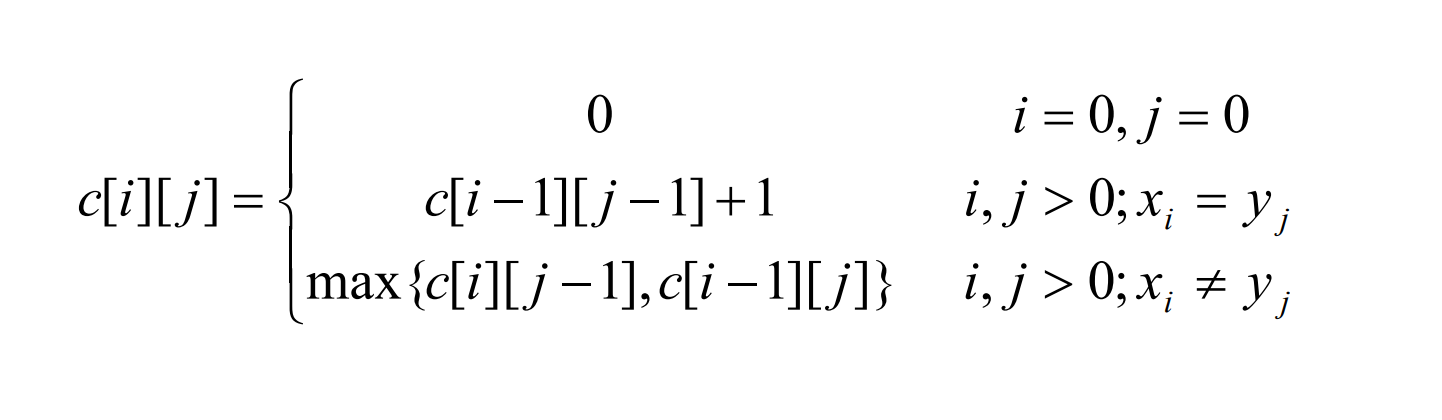
计算最优值：

由于在所考虑的子问题空间中，总共有θ(mn)个不同的子问题，
因此，用动态规划算法自底向上地计算最优值能提高算法的效率

void LCSLength(int m，int n，char *x，char *y，int **c，int **b)
{
int i，j;
for (i = 0; i <= m; i++) c[i][0] = 0;
for (i = 1; i <= n; i++) c[0][i] = 0;
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++) {
  if (x[i]==y[j]) {
     c[i][j]=c[i-1][j-1]+1; b[i][j]=1;}
  else if (c[i-1][j]>=c[i][j-1]) {
     c[i][j]=c[i-1][j]; b[i][j]=2;}
  else { c[i][j]=c[i][j-1]; b[i][j]=3; }
  }
}

【算法分析】 LCSlength算法中使用了两重循环，所以对于长度分别为m和n的序列，求其最长公共子序列的时间复杂度为O(m×n)。空间复杂度为O(m×n)

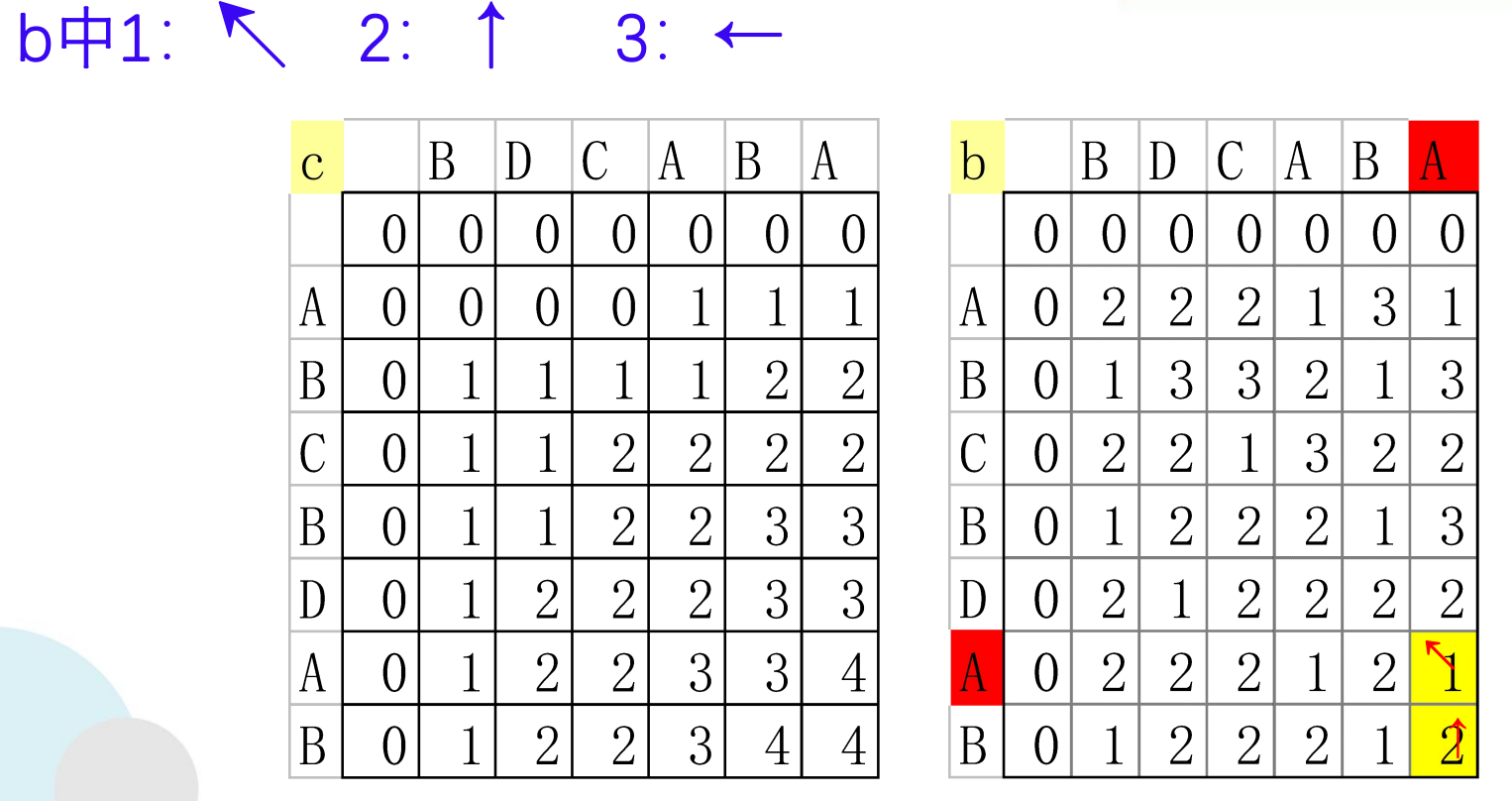
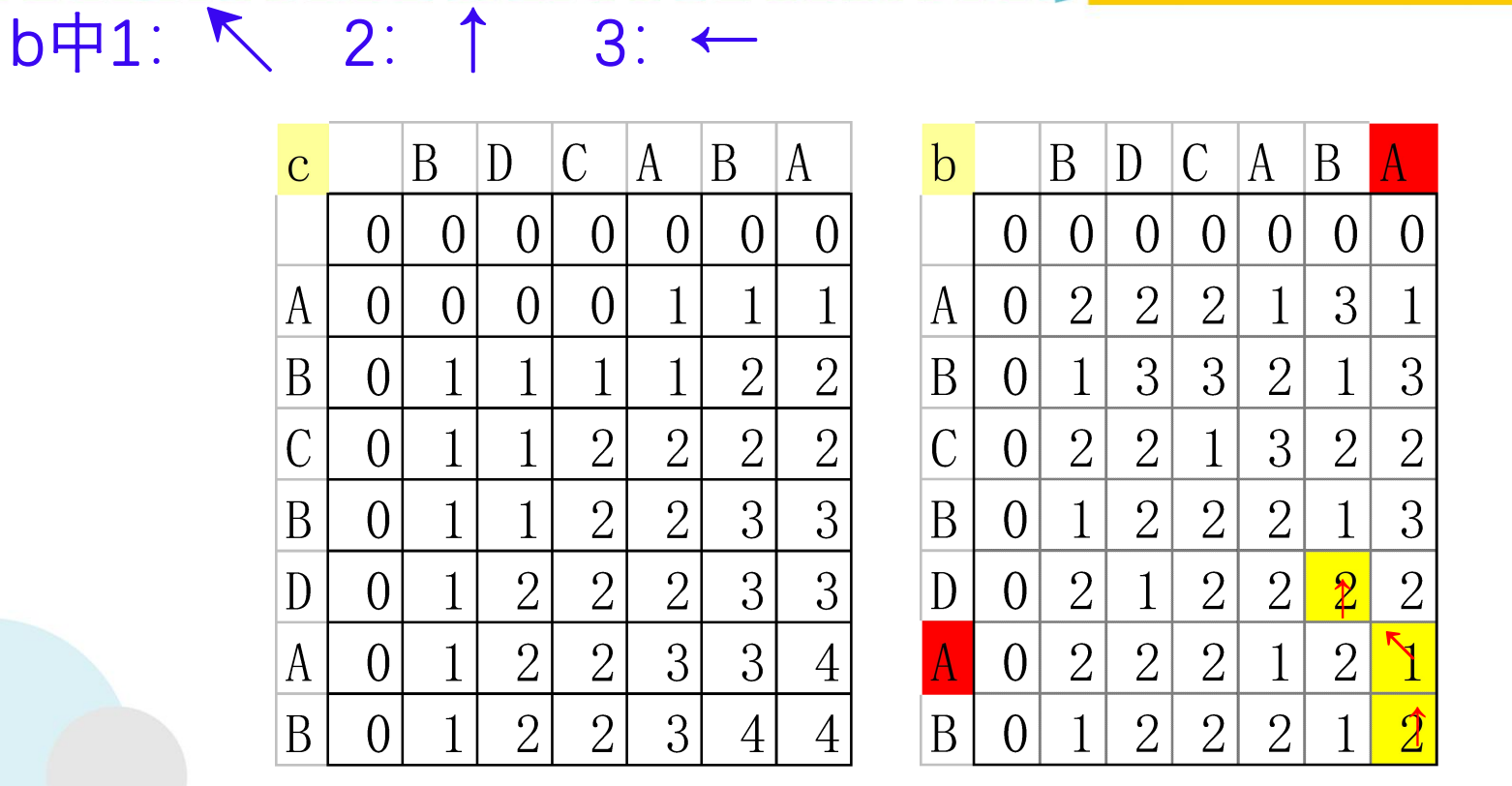
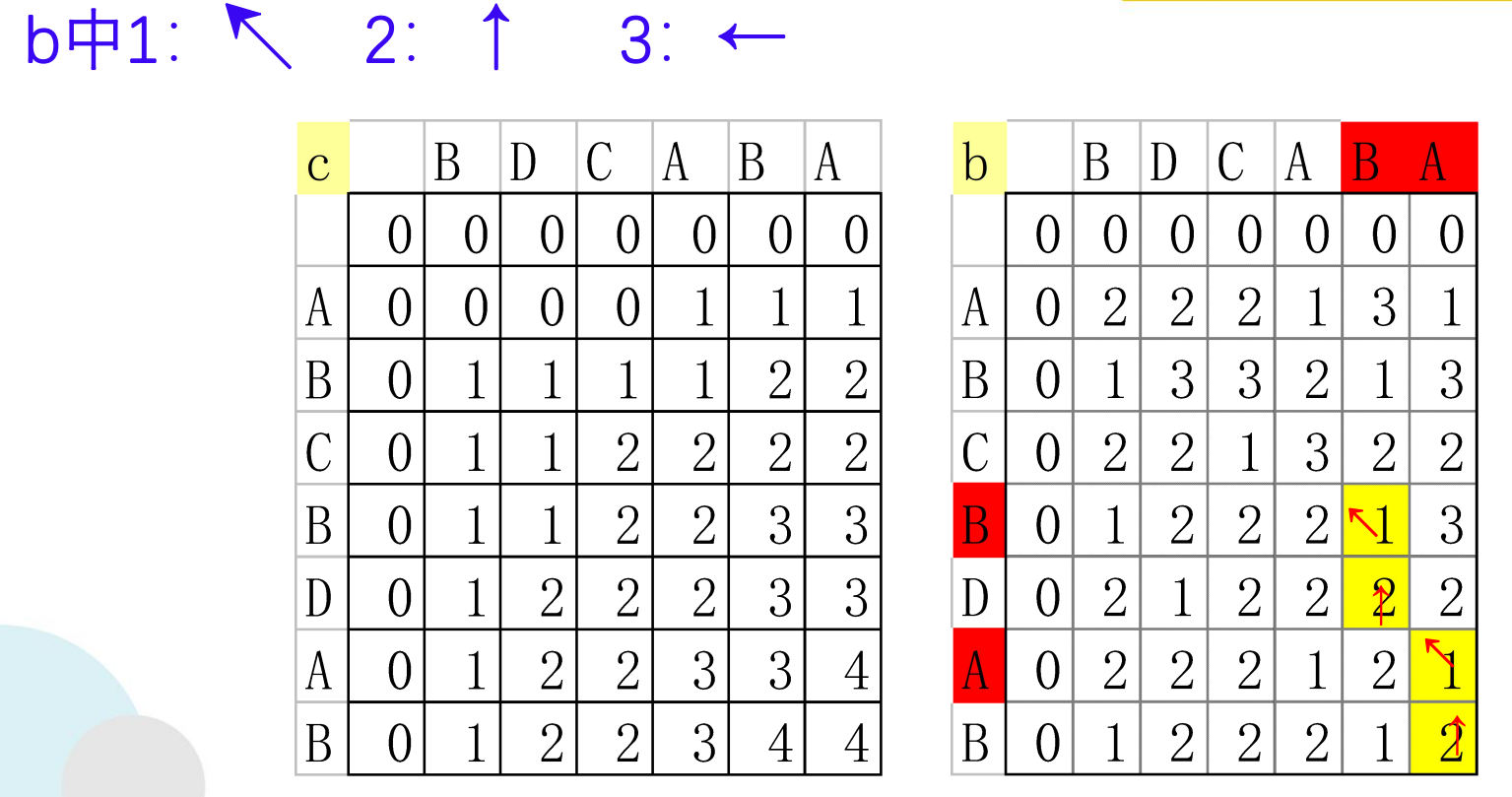
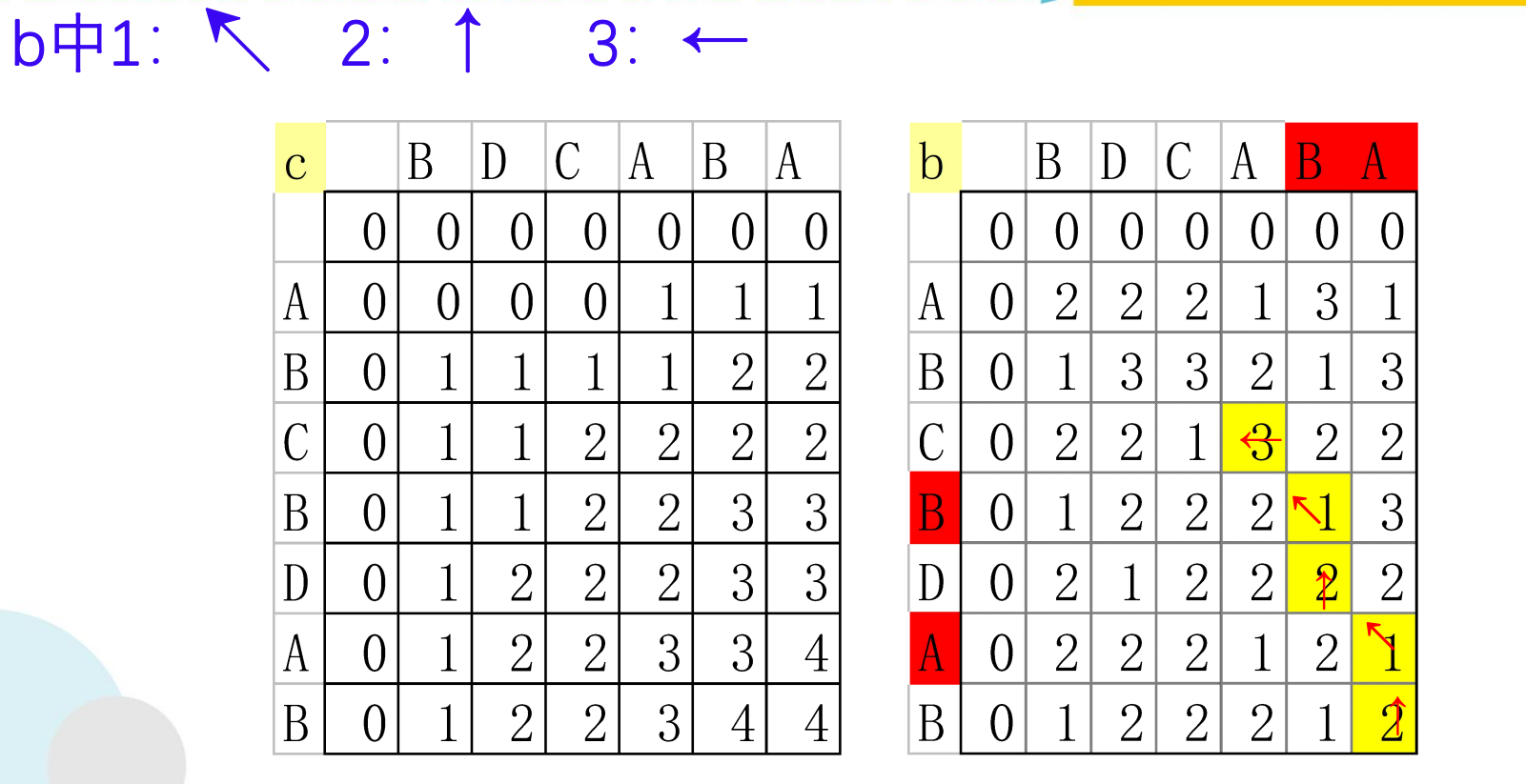
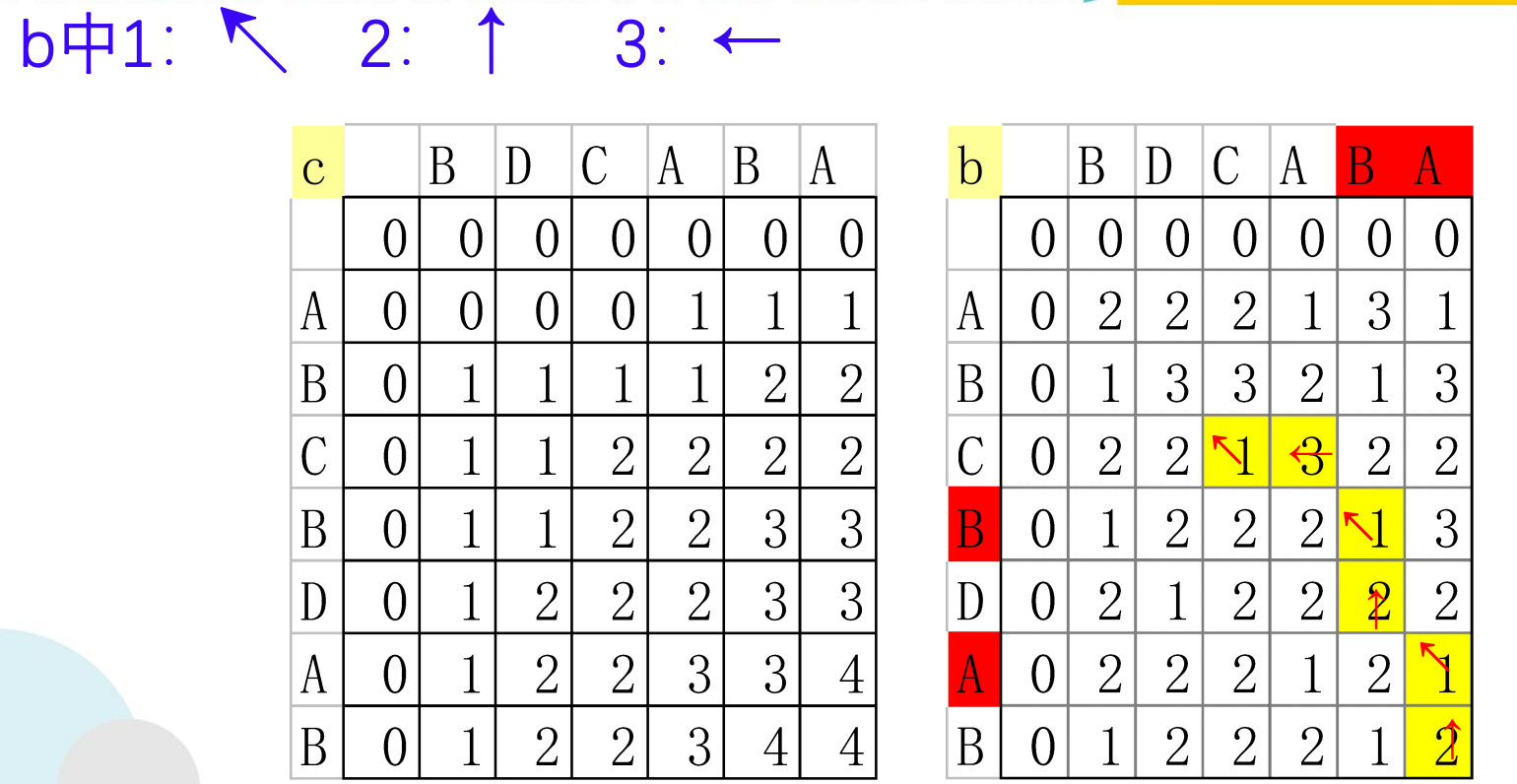
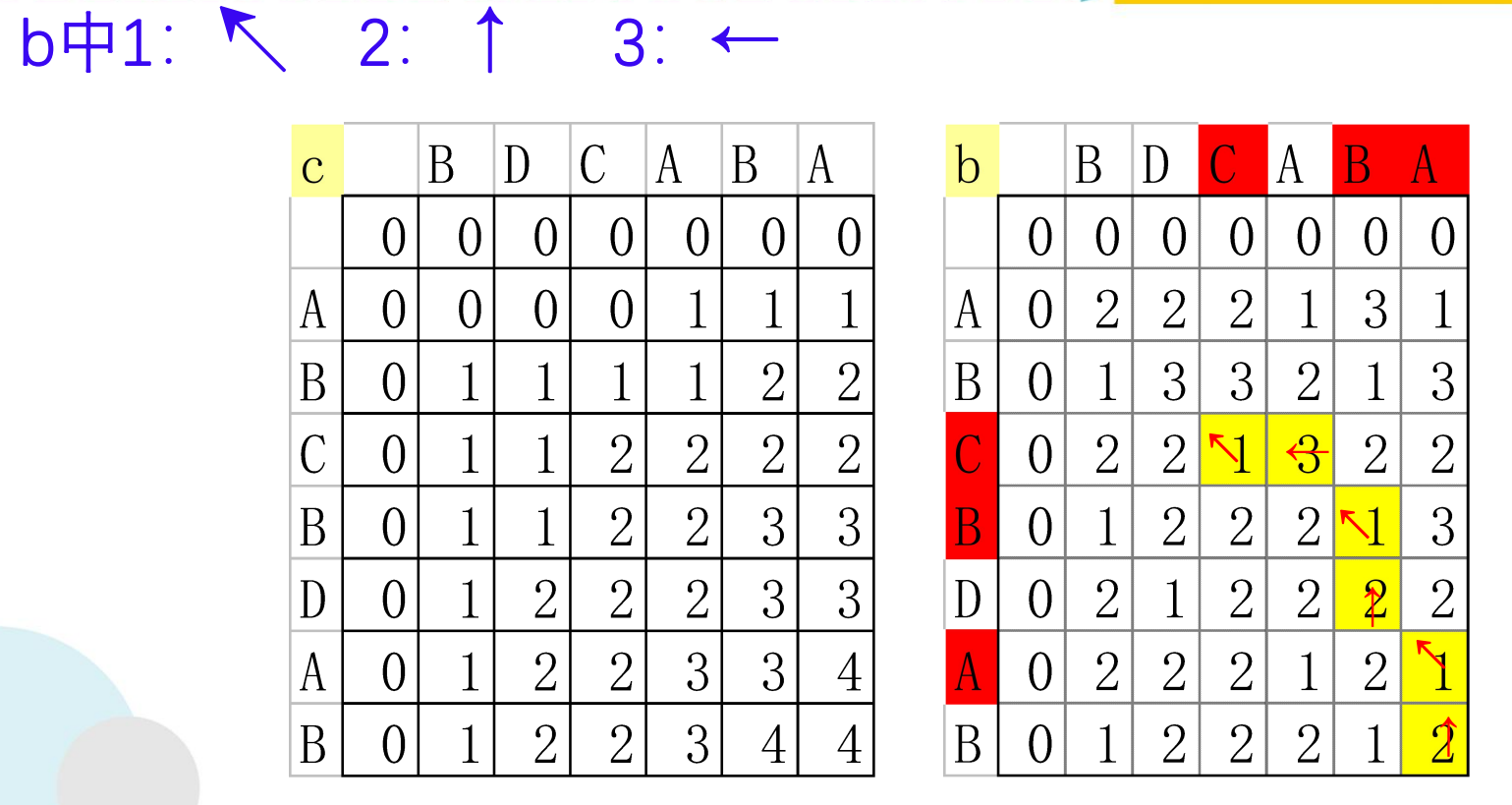
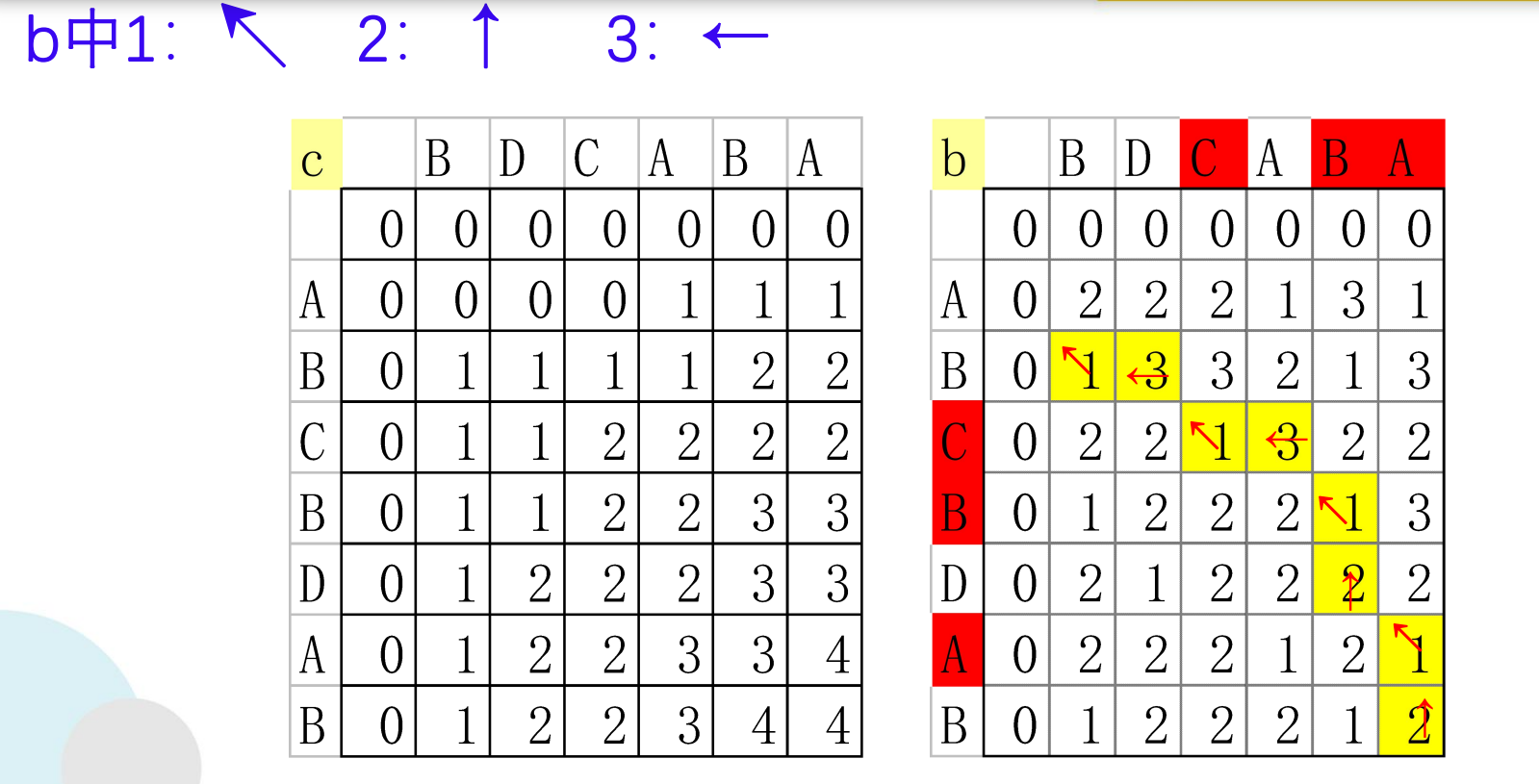
构造最长公共子序列

void LCS(int i，int j，char *x，int **b)
{
   if (i ==0 || j==0) return;
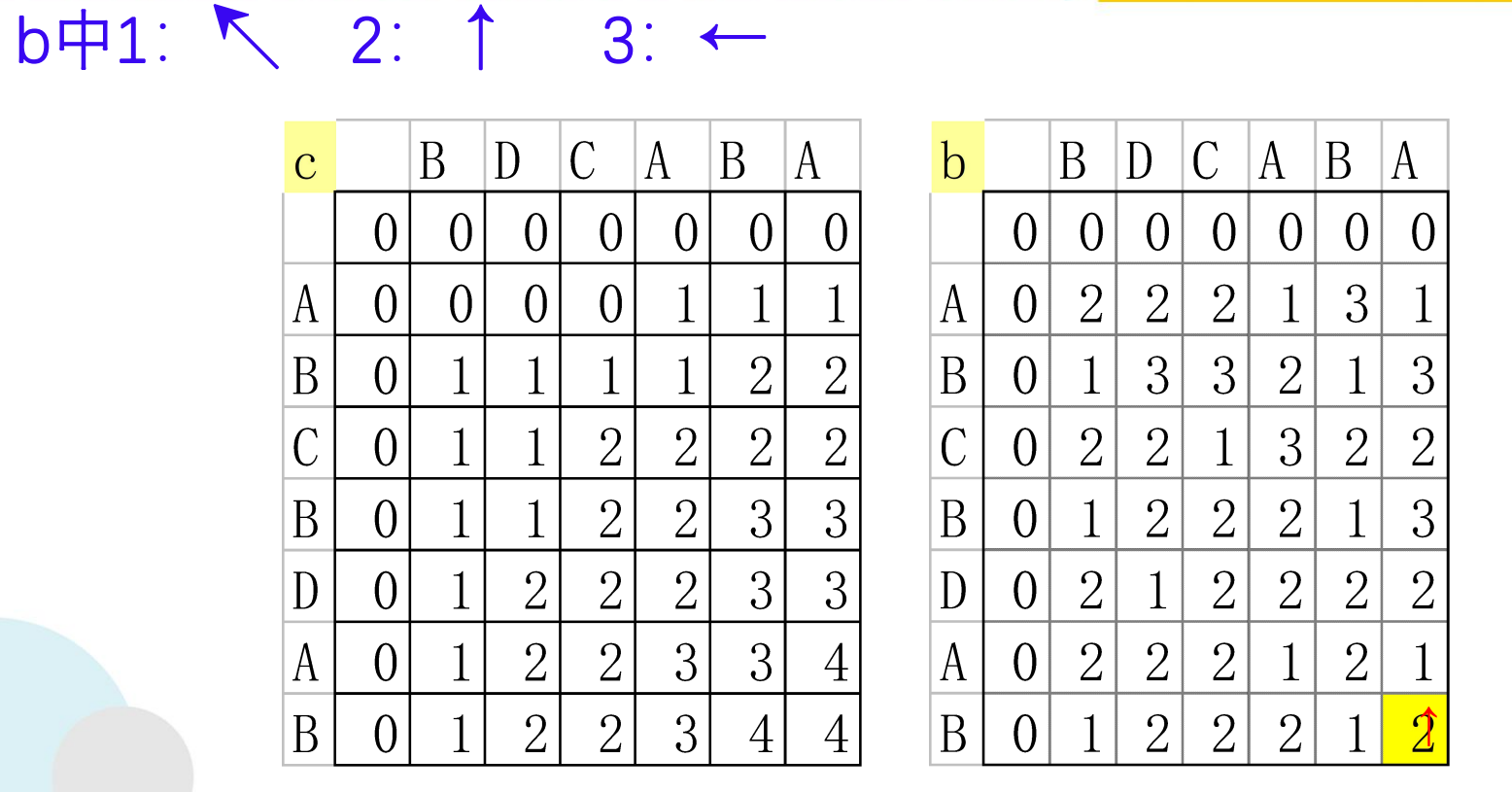
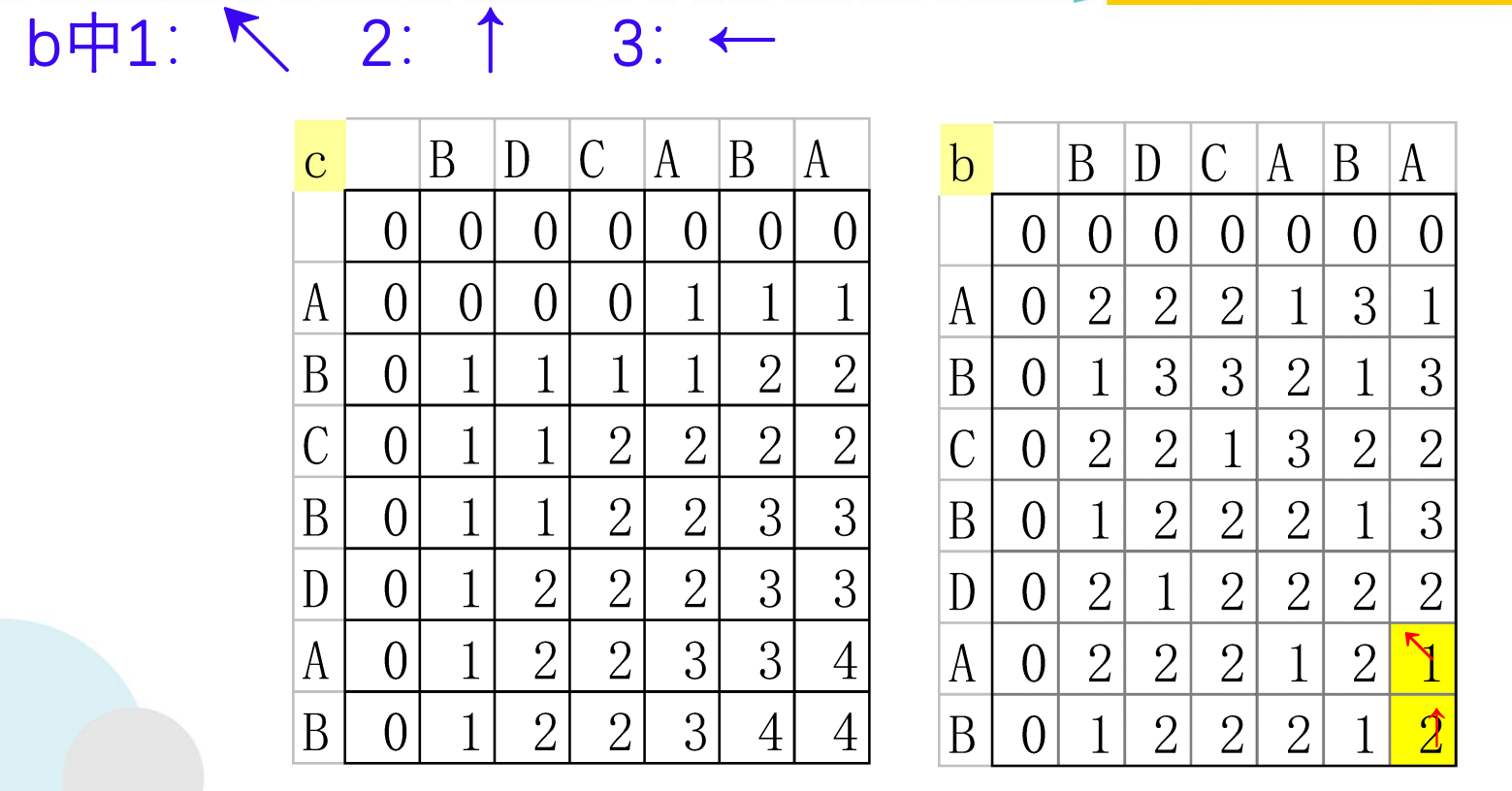
   if (b[i][j]== 1){ 
         LCS(i-1，j-1，x，b); //沿对角线方向，记为"↖ "
         cout<<x[i];
    } //第一个字符存放在x[1]，所以第i个字符存放在x[i]中
   else 
   if (b[i][j]== 2) LCS(i-1，j，x，b); //向上记为，记为"↑"
   else LCS(i，j-1，x，b); //向左记为，记为"←"
}

算法的改进

•在算法lcsLength和lcs中，可进一步将数组b省去。事实上，数组元
素c[i][j]的值仅由c[i-1][j-1]，c[i-1][j]和c[i][j-1]这3个数组元素的值所确定。
对于给定的数组元素c[i][j]，可以不借助于数组b而仅借助于c本身在时间内确定c[i][j]的值是由c[i-1][j-1]，c[i-1][j]和c[i][j-1]中哪一个值所确定的。
•如果只需要计算最长公共子序列的长度，则算法的空间需求可大大减少。事实上，在计算c[i][j]时，只用到数组c的第i行和第i-1行。因此，用2行的数组空间就可以计算出最长公共子序列的长度。进一步的分析还可将空间需求减至O(min(m,n))