找出问题的解集或什么解是满足约束条件的最佳解->回溯法
回溯法:搜索,或避免不必要搜索的穷举式搜索法。适用于解一些组合数相当大的问题。
在解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至任意一点时,先判断该结点是否包含问题的解。
如果肯定不包含,则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。
基本思想
回溯法:类似穷举的搜索尝试过程,是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”(即回退),尝试别的路径。
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发搜索解空间树。
首先根结点成为活结点(自身已生成但其孩子结点没有全部生成的结点),同时也成为当前的扩展结点(正在产生孩子结点的结点)。
在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为新的活结点,并成为当前扩展结点。
如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点(由根结点到该结点构成的部分解不满足约束条件,或者其子结点已经搜索完毕)。
此时应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。
回溯法以这种方式递归地在解空间中搜索,直至找到所要求的解或解空间中已无活结点为止。
问题的解空间
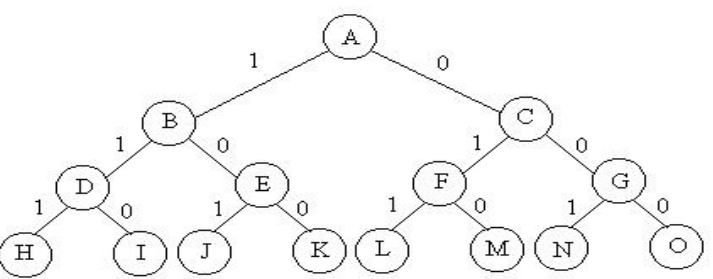
•解向量:问题的解能够表示成一个n元式(x1,x2,…,xn)的形式。
•解空间:所有满足约束条件的解向量组构成了问题的解空间。
•解空间树:问题的解空间一般用树形式来组织,也称为解空间树或状态空间,树中的每一个结点确定所求解问题的一个问题状态。
•例如,对于有n种可选择物品的0-1背包问题,当n=3时,其解空间是
{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)}
问题的解空间树
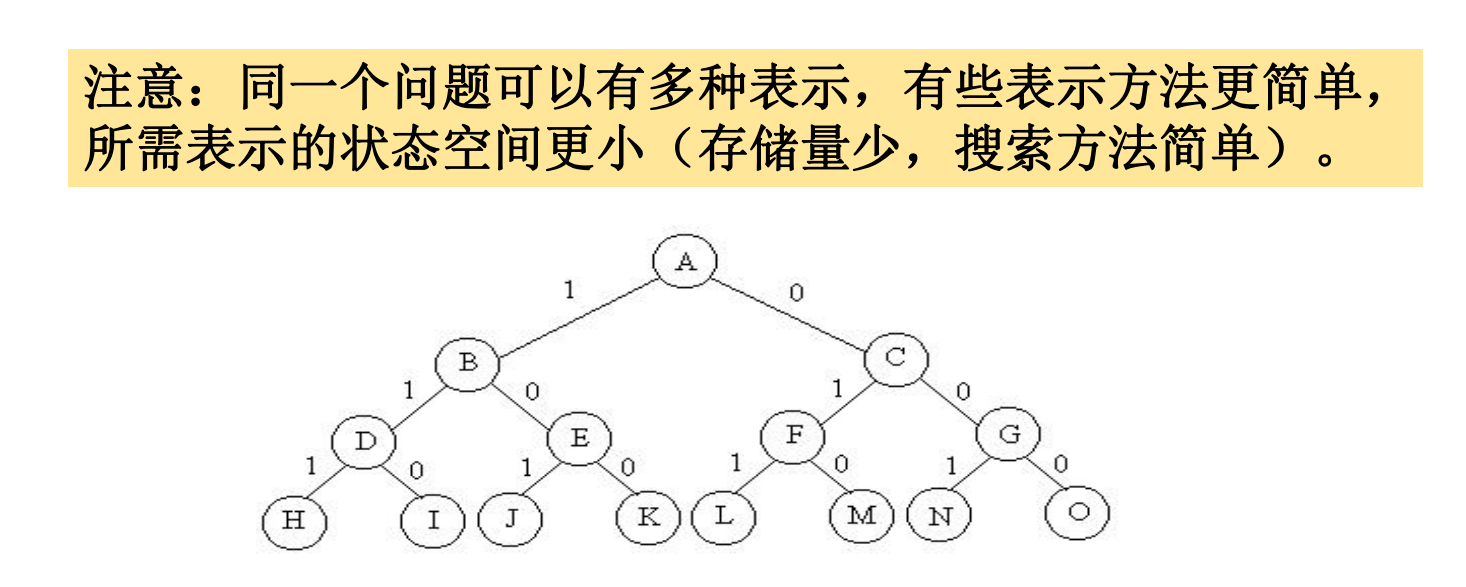
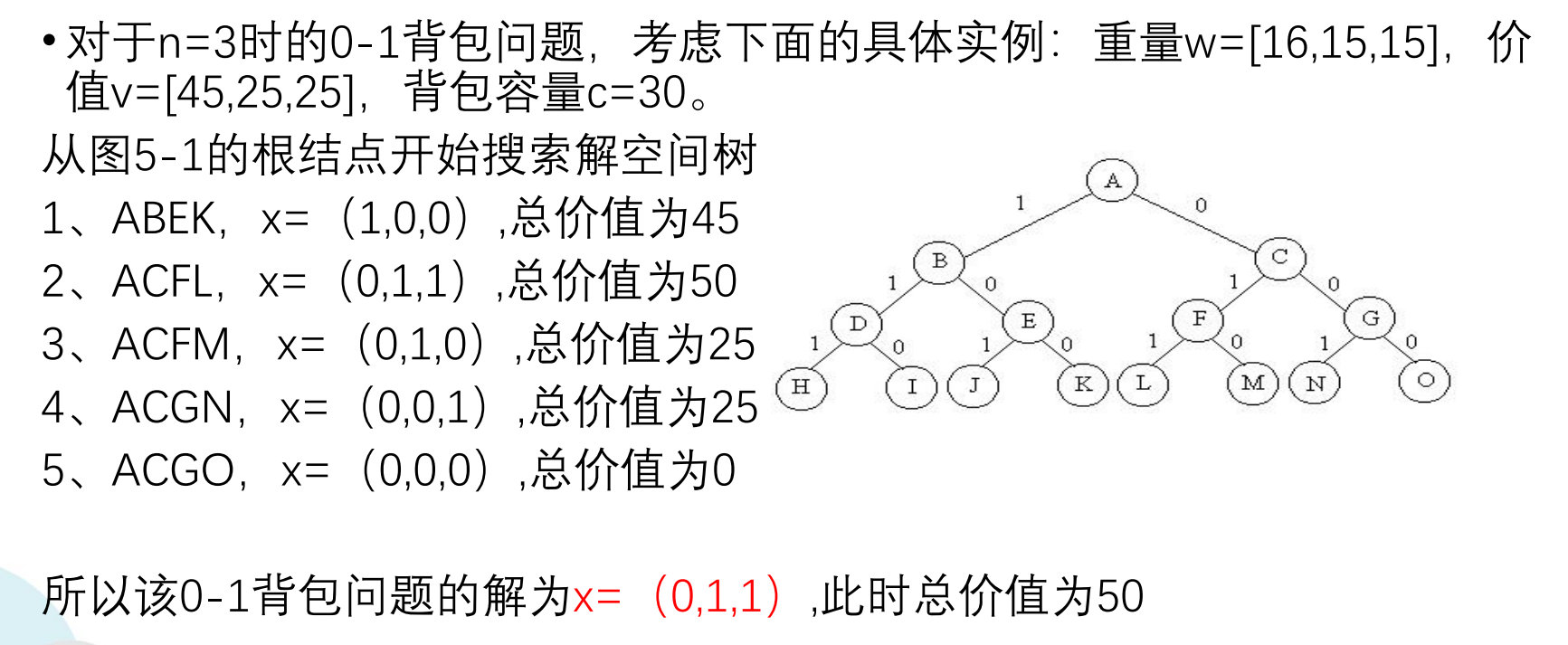
回溯法的解题步骤
根据上面0-1背包问题的例子,我们可以总结出回溯法解题的3大步骤:
(1)针对所给问题,定义问题的解空间;
(2)确定易于搜索的解空间结构;
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
常用剪枝函数:
用约束函数在扩展结点处剪去不满足约束的子树;
用限界函数剪去得不到最优解的子树
• 用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。
• 在任何时刻,算法只保存从根结点到当前扩展结点的路径。
• 如果解空间树中从根结点到叶结点的最长路径的长度为h(n),则回溯法所需的计算空间通常为O(h(n))。
• 而显式地存储整个解空间则需要O(2^h(n))或O(h(n)!)内存空间
旅行售货员问题
下面我们用回溯法的3大解题步骤来解旅行售货员问题
•某售货员要到若干城市去推销商品,已知各城市之间的路程(旅费),他要选定一条从驻地出发,经过每个城市一遍,最后回到驻地的路线,使总的路程(总旅费)最小。
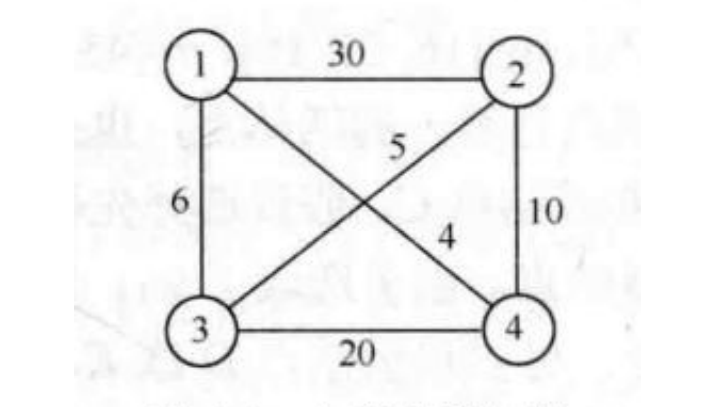
第一步,定义问题的解空间
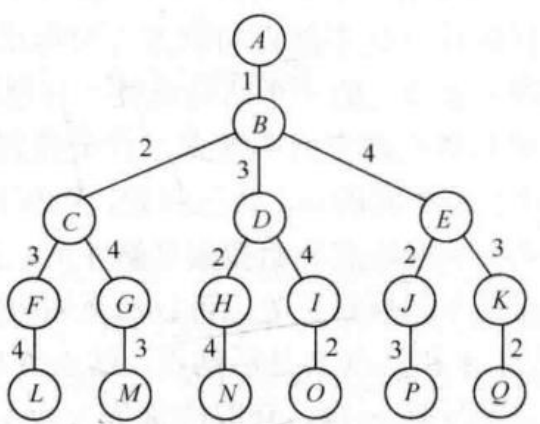
旅行售货员问题的解空间是
• 1,2,3,4,1
• 1,2,4,3,1
• 1,3,2,4,1
• 1,3,4,2,1
• 1,4,2,3,1
• 1,4,3,2,1
第二步,确定解空间树
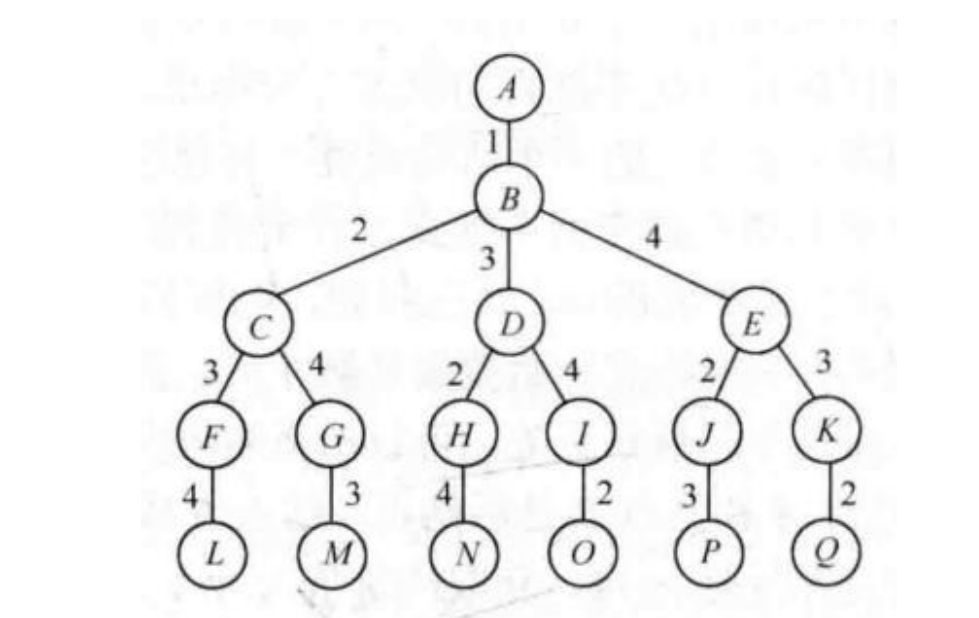
第三步,以深度优先搜索解空间树

回溯法的基本术语
• 活结点是指自身已生成但其孩子结点没有全部生成的结点
• 扩展结点是指正在产生孩子结点的结点
• 死结点是指由根结点到该结点构成的部分解不满足约束条件,或者其子结点已经搜索完毕
回溯法搜索解空间时,采用剪枝函数避免无效搜索,提高回溯的搜索效率:
• 用约束函数在扩展结点处剪除不满足约束的子树;
• 用限界函数剪去得不到问题解或最优解的子树。
• 子集树:当所给的问题是从n个元素的集合S中找出满足某种性质的子集时,相应的解空间树称为子集树。
• 排列树:当所给的问题是确定n个元素满足某种性质的排列时,相应的
解空间树称为排列树
回溯法的算法框架
非递归回溯框架(迭代回溯)
int x[n]; //x存放解向量,全局变量
void Iterativebacktrack(void) //非递归框架
{
int t=1; //根结点层次为1
while (t >0) //尚未回溯到头
{
if(f(n,t)<=g(n,t)) //当前结点存在子结点
{
for (int i=f(n,t);i<=g(n,t);i++) //用i枚举t所有可能的路径
{
x[t]=h(i) //产生一个可能的解分量 h(i)
if (constraint(t) && bound(t))
//x[i]满足约束条件或限界函数
{
if (solution(t)) output(x); //到达叶子结点,输出一个可行解x
else t++; //否则深度遍历下一层次
}
}
}
else t--; //回溯:不存在子结点,返回上一层
}
}子集树递归算法框架

int x[n]; //x存放解向量,全局变量
void backtrack(int t) //求解子集树的递归框架
{
if(t>n)Output(x); //搜索到叶子结点,输出一个可行解
else
{ for (int i=0;i<=1;i++) //用i枚举t所有可能的路径
{ x[t]=i; //产生一个可能的解分量
… //其他操作
if (constraint(t) && bound(t))
backtrack(t+1); //满足约束条件和限界函数,继续下一层
}
}
}排列树递归算法框架
遍历排列树需要O(n!)计算时间
int x[n]; //x存放解向量,并初始化
void backtrack(int t) //求解排列树的递归框架
{
if(t>n)Output(x); //搜索到叶子结点,输出一个可行解
else
{ for (int i=t;i<=n;i++) //用i枚举t所有可能的路径
{ … //第t层的结点选择x[i]的操作
swap(x[t],x[i]); //为保证排列中每个元素不同,通过交换来实现
if (constraint(t) && bound(t))
backtrack(t+1); //满足约束条件和限界函数,进入下一层
swap(x[t],x[i]); //恢复状态
… //第t层的结点选择x[i]的恢复操作
}
}
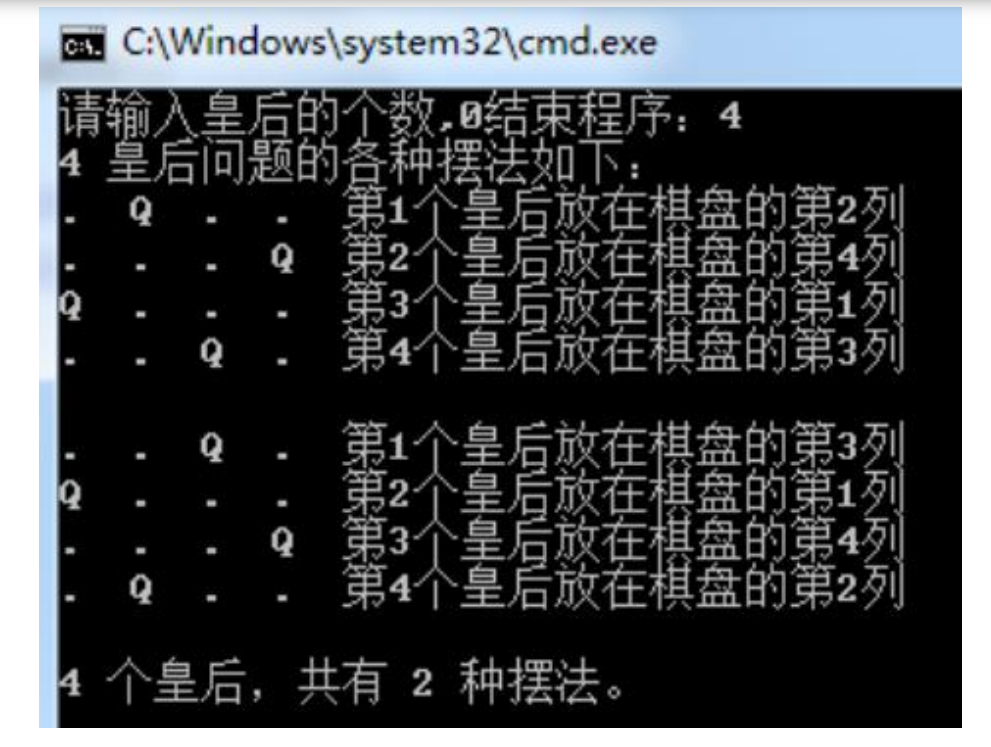
}n皇后问题
1.判断解是否可行的条件
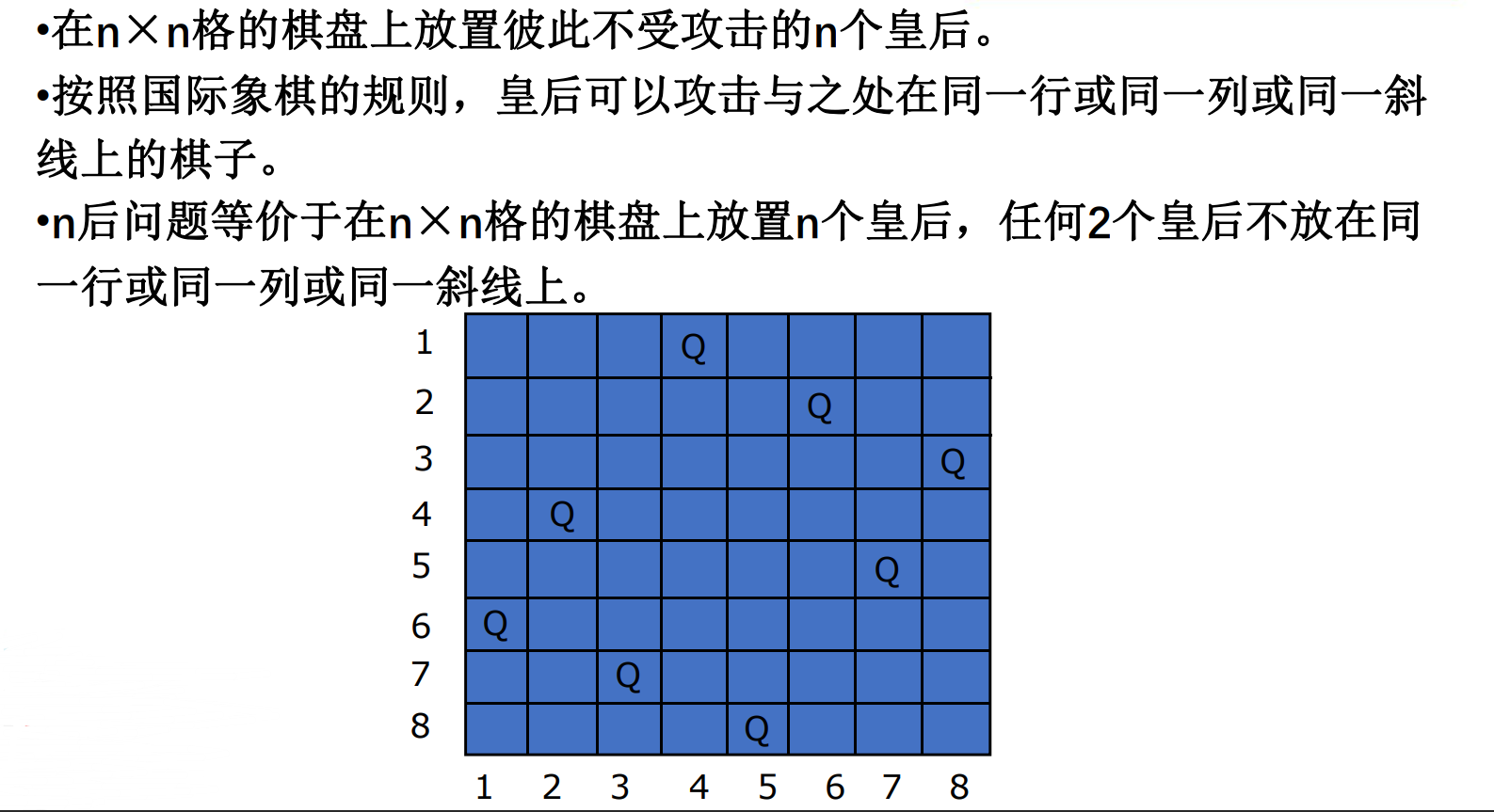
我们从第一行开始放皇后,第一行有n个位置可以放,我们用x1来表示第一行的皇后所在的列,第二行有n-1个位置可以放,我们用x2来表示第二行皇后所在的列······因此,我们用一个数组x[n]来表示问题的解,x[i]表示皇后i放在第i行第x[i]列。
如何保证任何两个皇后不同一行,不同一列?
x[i]表示皇后i放在第i行第x[i]列。
x[k]表示皇后k放在第k行第x[k]列。
不同一行:i≠k
不同一列:x[i]≠x[k]
如何保证任何两个皇后不同一条斜线上?
设两个皇后q1和q2放在(i,j)和(k,l)位置上,如果q1和q2在斜率为-1的对角线上,那么i - j = k - l成立。
如果在斜率为1的对角线上,那么i + j = k + l成立,由此可知只要 | i - k |≠ | j - l |成立,q1和q2就不再同一条斜线上。| i - k | ≠ | j
2.确定解空间
用完全n叉树表示解空间,现在以n=4为例:
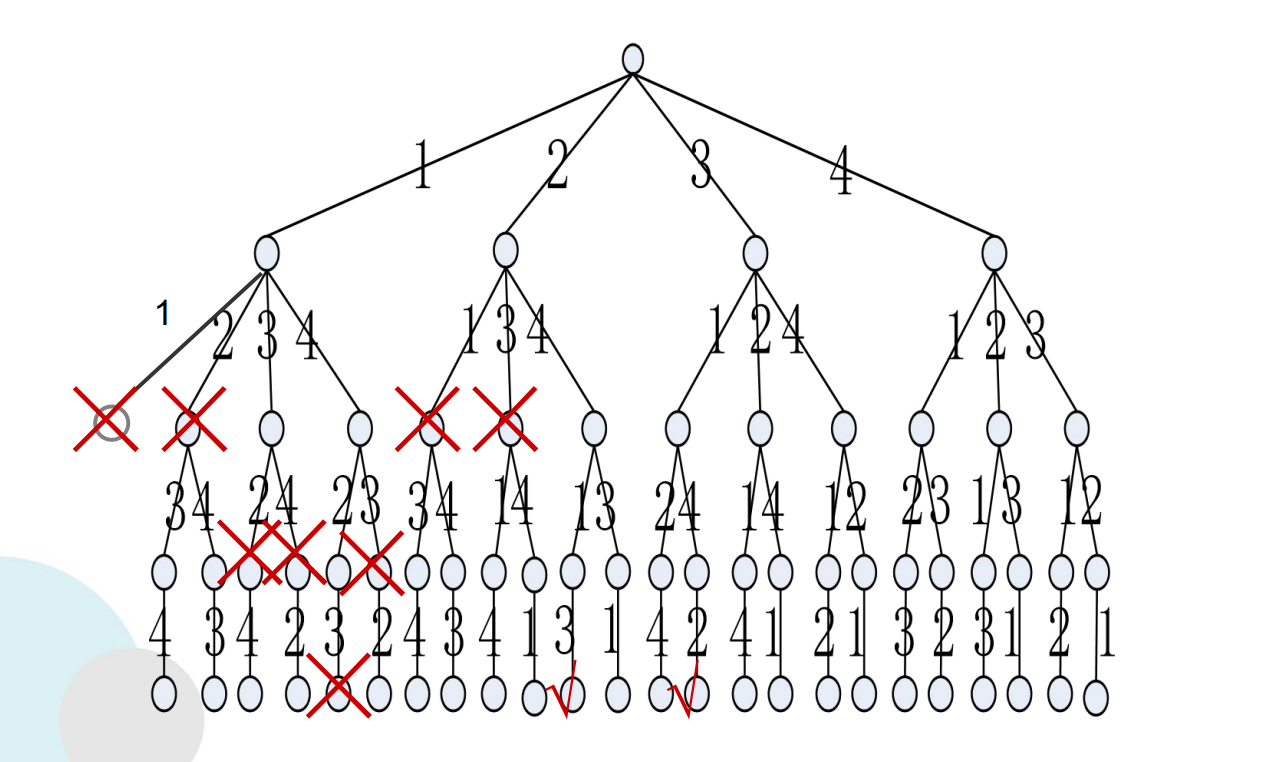
皇后问题的解为:

此处评论已关闭