BFS:Breadth First Search 广度优先搜索
DFS:Depth First Search 深度优先搜索

为了搜索 DFS，我们使用堆栈，为了搜索 BFS，我们使用队列。

广度优先搜索(BFS)

广度优先搜索(BFS):广度优先搜索构建一个广度优先的树，最初只包含它的根，也就是源顶点 s。每当搜索在扫描已经发现的顶点 u 的邻接表的过程中发现一个白色顶点 v 时，顶点 v 和边(u，v)就被添加到树中。我们说 u 是广度优先树中 v 的前
身或母体。因为顶点最多被发现一次，所以它最多有一个父顶点。广度优先树中的祖先和后代关系通常是相对于根 s 定义的:如果 u 在树中从根 s 到顶点 v 的简单路径上，那么 u 是 v 的祖先，v 是 u 的后代





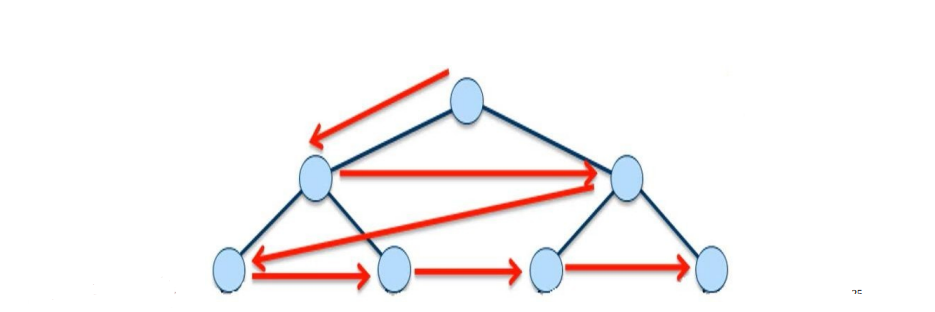
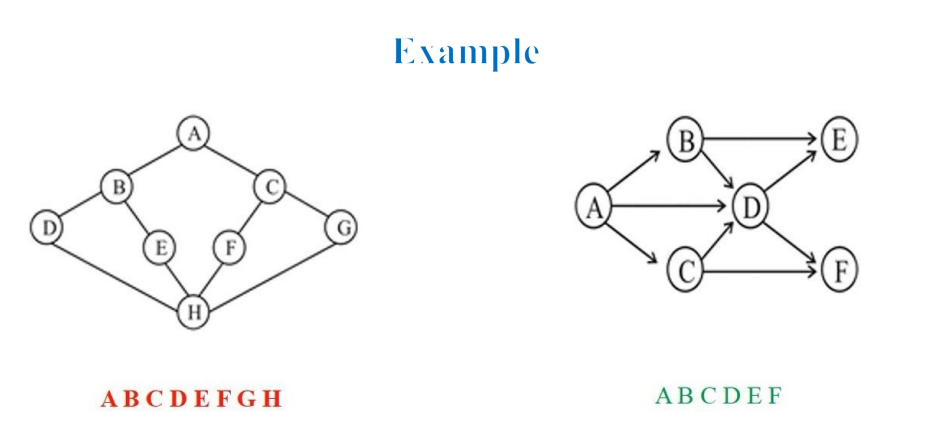
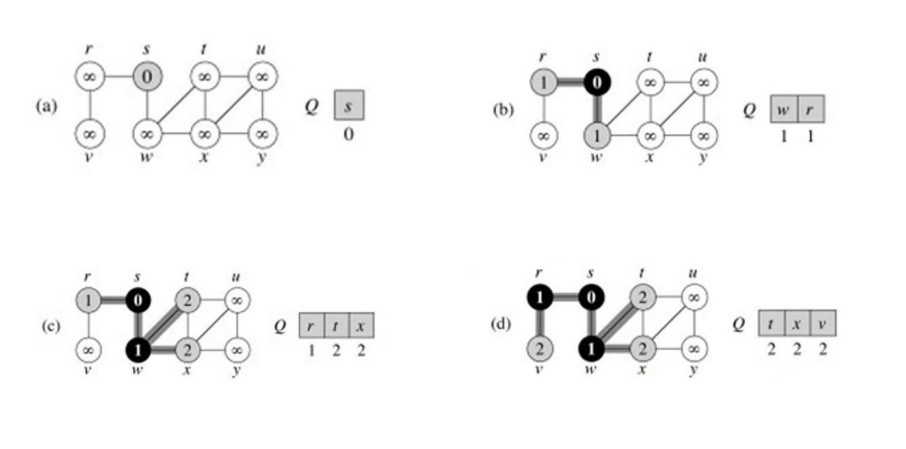
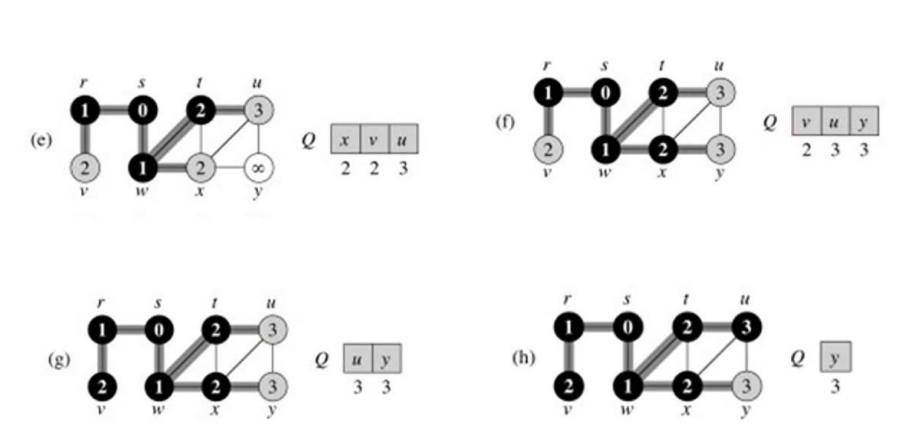
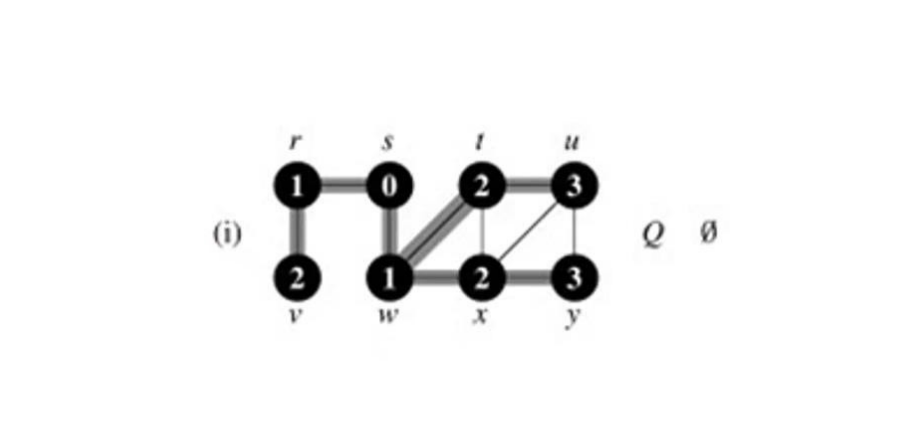
BFS 算法的复杂性，取决于你是如何实现算法的。如果你用邻接矩阵来实现，那么复杂度就是O(n^2).如果你是通过邻接
表实现的，那么复杂度将是O(V+E)，其中E是边的数量。

graph={
    'a':['b','c'],
    'b':['a','c','d'],
    'c':['a','b','d','e'],
    'd':['b','c','e','f'],
    'e':['c','d'],
    'f':['d']
}

def BFS(graph, s):
    queue = []
    queue.append(s)
    seen = set()
    seen.add(s)
    while(len(queue) > 0):
        v = queue.pop(0)
        nodes = graph[v]
        for w in nodes:
            if w not in seen:
                queue.append(w)
                seen.add(w)
        print(v)

BFS(graph, 'a')

深度优先搜索：DFS

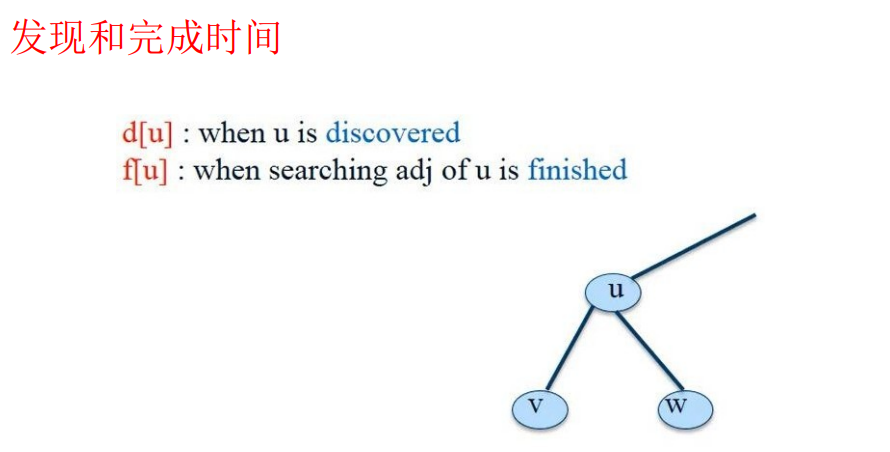
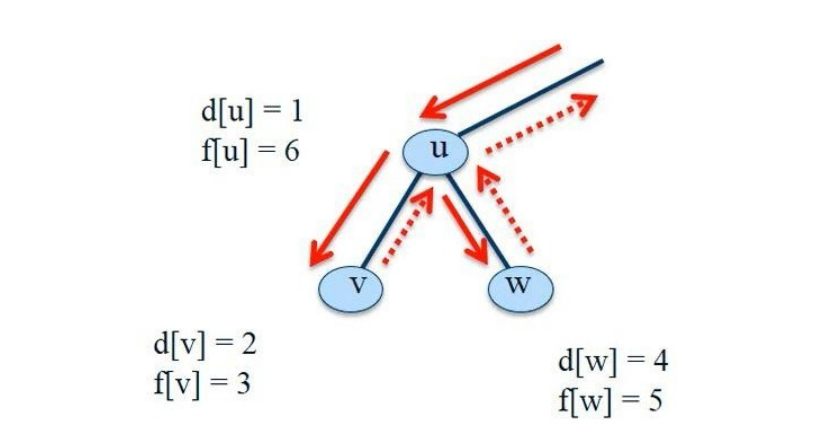
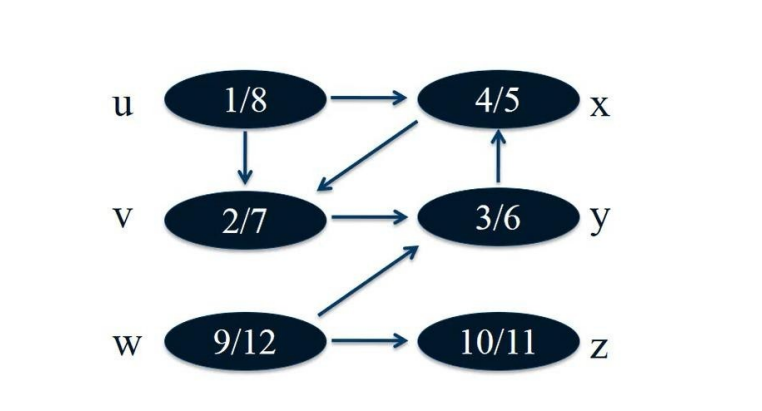
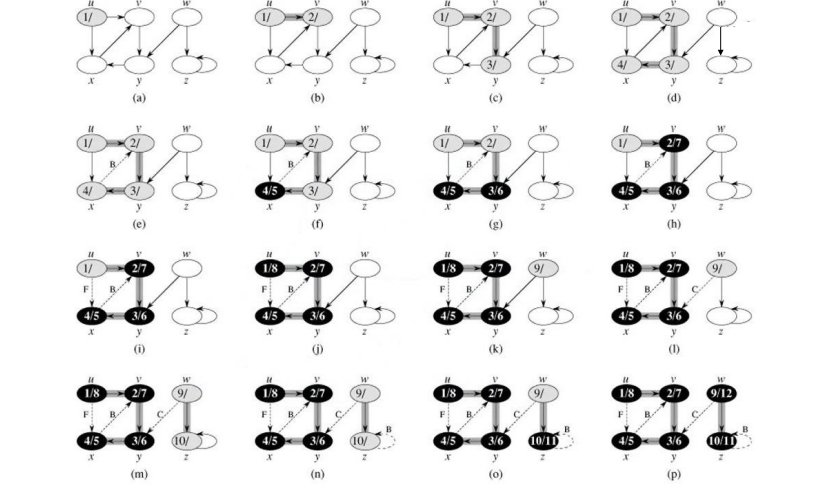
与广度优先搜索一样，深度优先搜索在搜索过程中对顶点进行着色，以指示它们的状态。每个顶点最初都是白色的，当在搜索中发现它时，它是灰色的，当它完成时，也就是说，当它的邻接表被完全检查时，它是黑色的。这种技术保证了每个顶点恰好在一个深度优先的树中结束，因此这些树是不相交的。除了创建深度优先的森林，深度优先搜索还会为每个顶点添加时间戳。每个顶点 v 都有两个时间戳:第一个时间戳 v.d 记录了第一次发现 v 的时间(并呈灰色)，第二个时间戳 v.f 记录了搜索完成检查 v 的邻接表的时间(并使 v 变黑)。这些时间戳提供了关于图结构的重要信息，通常有助于推理深度优先搜索的行为。

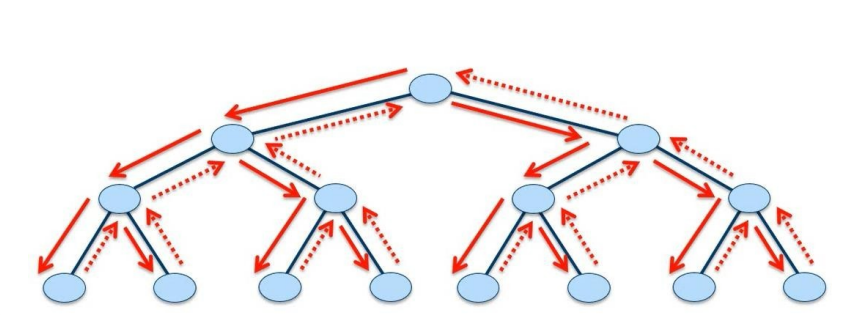
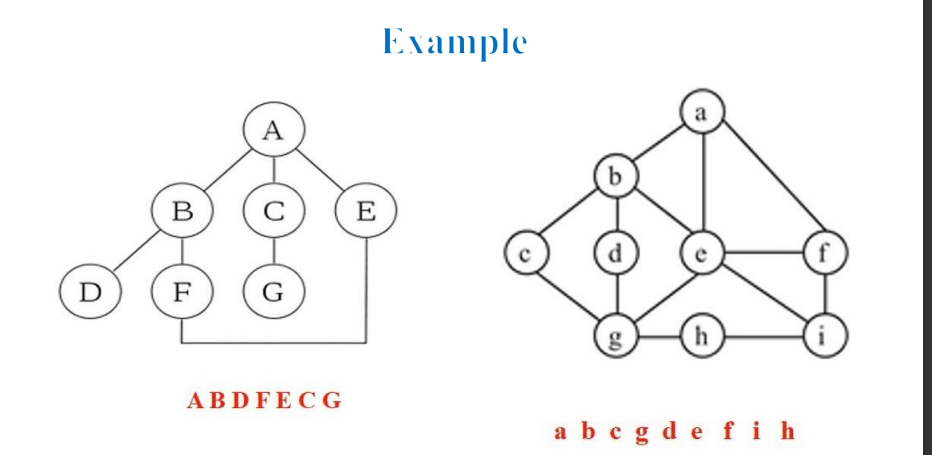
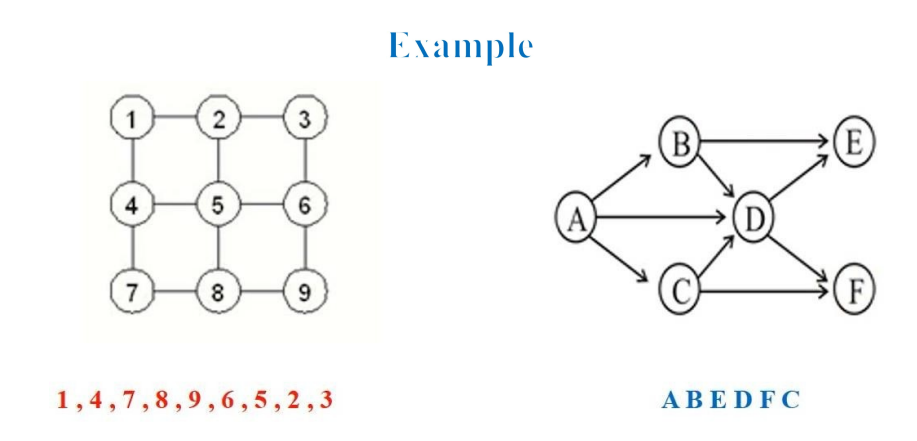
graph1 = { 
    'A' : ['B','S'], 
    'B' : ['A'], 
    'C' : ['D','E','F','S'], 
    'D' : ['C'], 
    'E' : ['C','H'], 
    'F' : ['C','G'], 
    'G' : ['F','S'], 
    'H' : ['E','G'], 
    'S' : ['A','C','G'] 
} 

def dfs(graph, node, visited): 
    if node not in visited: 
     visited.append(node) 
     for n in graph[node]: 
      dfs(graph,n, visited) 
    return visited 

visited = dfs(graph1,'A', []) 
print(visited)