先来介绍一下哈夫曼编码吧
哈夫曼树，二叉树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。哈夫曼编码则是根据字符出现频率(权重分布)，用最少的位数来表示。
(字符出现多的，用较短编码；字符出现少的，用较长编码)。
举个例子：好比这个字符串“abcddddddd”，如果用相同长度的编码来表示，4个不同数字则选用2位
(a->00,b->01,c->10,d->11)，那也就是需要 10 2 = 20长度；
而使用哈夫曼编码，则根据权重(a->010,b->011,c->00,d->1)，也就是需要:3+3+2+17 = 15长度。
在这个例子中相比平均编码则少了25%(当然这个例子比较夸张啦哈哈哈。权重分布一般不会这样，在这里主要是想说明哈夫曼编码能起到压缩编码长度的作用),但是在取哈夫曼编码的时候，要避开前缀(有可能某个数的编码刚好是另外某个数的编码前缀)，所以可以通过下面的方法计算出来。

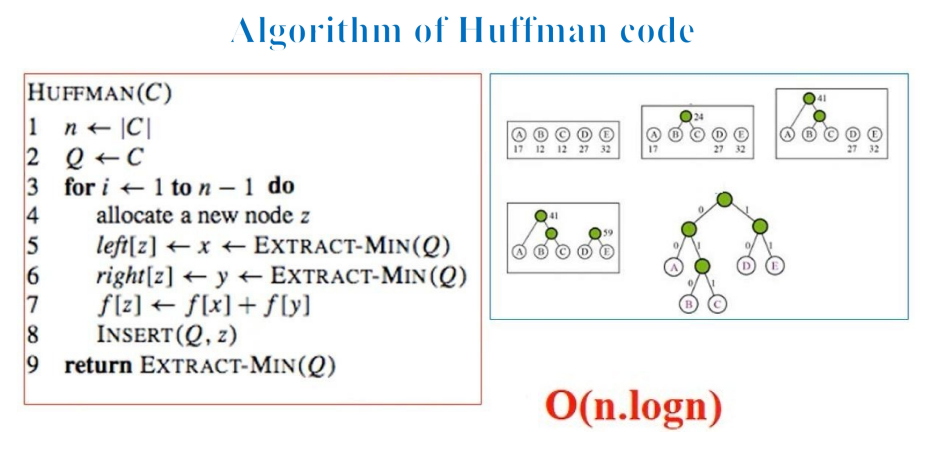
一、基于建哈夫曼树的方法
算法过程：
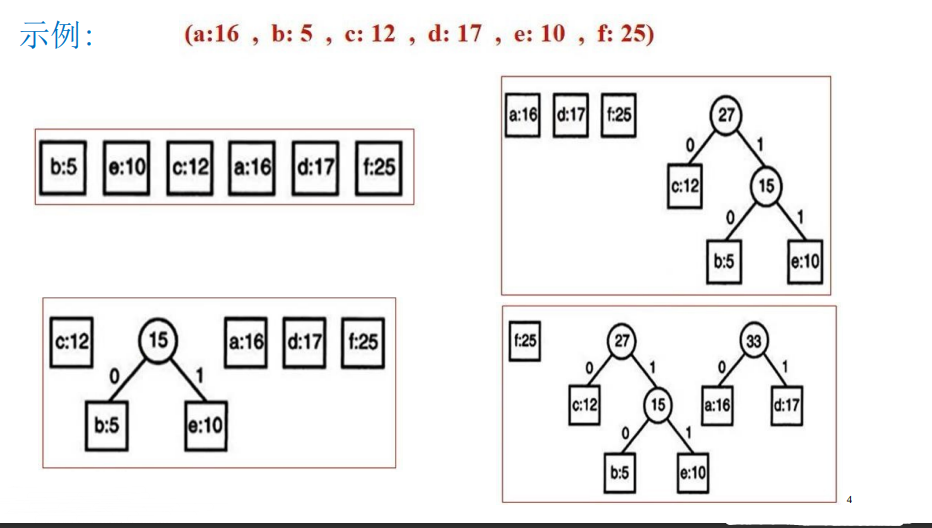
①将输入的数值，每一个数值，分别都建立成一棵树(只有根节点的树)，就形成了森林。
②将森林排序( 按权重，从大到小排序，选用插入排序即可，因为之后的排序每一次都只插入一个数值，只需要移动少量即可)
③取出后两棵树n1、n2，新创建一个根节点，然后将n1、n2作为其左右孩子，从而构成一棵新树(由新建根节点+n1(lchild)+n2(rchild)组成)，将这棵新树插入森林中。
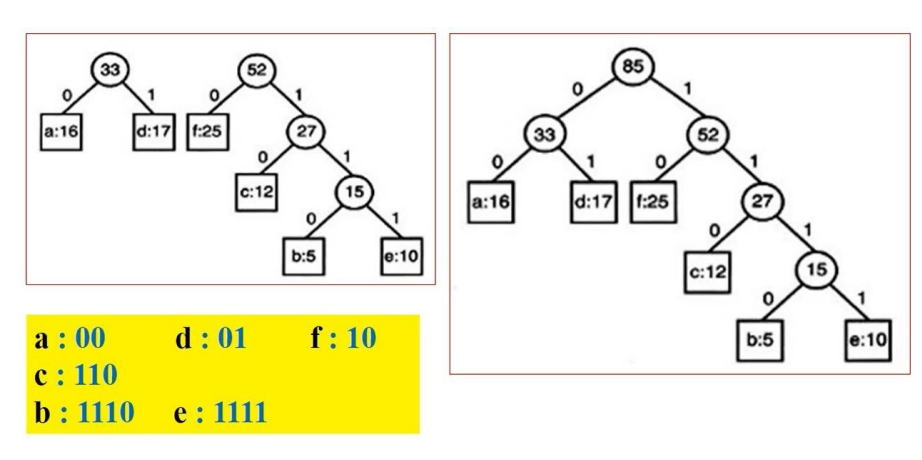
④重复②③，直到森林中只剩下一棵树，此时该树就是所求哈夫曼树。
⑤遍历每一个叶子(每一个叶子就是输入数值)，根据遍历路径(往lchild则 +‘1’，往rchild 则 + ‘0’)，每一个叶子对应的数值+编码result，即是其哈夫曼编码。